1.066.444
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát
Villamosságtan 6.
Általános hálózategyenletek/Budapesti Műszaki Egyetem Villamosmérnöki Kar/Kézirat
Budapest
| Kiadó: | Tankönyvkiadó Vállalat |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Ragasztott papírkötés |
| Oldalszám: | 160 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 24 cm x 17 cm |
| ISBN: | |
| Megjegyzés: | Kézirat. Tankönyvi szám: J 5-1062. 99 fekete-fehér ábrával illusztrálva. A könyv 364 példányban jelent meg. |
Értesítőt kérek a kiadóról
A beállítást mentettük,
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
A beállítást mentettük,
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Előszó
A következőkben olyan fogalmakat ismertetünk, amelyek felhasználásával lehetséges a hálózat felépítésének matematikai leírása.1.1 Gráfok és részgráfok
A hálózat gráfja a hálózat ágainak és... Tovább
Előszó
A következőkben olyan fogalmakat ismertetünk, amelyek felhasználásával lehetséges a hálózat felépítésének matematikai leírása.1.1 Gráfok és részgráfok
A hálózat gráfja a hálózat ágainak és csomópontjainak egymáshoz illeszkedését jellemzi függetlenül attól, hogy az ágakat milyen hálózati elemek alkotják.
Ha a hálózat elemeit az ábrázolásnál egy-egy vonaldarabbal helyettesítjük úgy, hogy az elemek egymással összekötött pontjának a megfelelő vonalak közös pontja felel meg és a vonalaknak más közös pontja nincs, akkor a hálózat egy gráfját ábrázoltuk. A hálózat ágainak a gráf ágai (élei), az ágak csatlakozási pontjainak a gráf csomópontjai (csúcsai) felelnek meg. Az 1.1 a. ábrán látható hálózat egy gráfját az 1.1 b. ábrán vázoltuk. A gráf éleit és csúcsait sorszámmal látjuk el. A csúcsok sorszámát zárójelbe tesszük.
A csomóponthoz csatlakozó elemek száma megadja a csomópont fokszámát. (Pl. az 1.2 ábrán a csomópont fokszáma 4.)
A csomóponthoz csatlakozó ágakat a csomóponthoz, a csomópontot az ághoz illeszkedőnek is mondjuk. Pl. az 1.1 b ábrán látható gráf (1) csomópontjához az 1, 2, 4, 5 jelű ág, a 3 jelű ághoz a (2) és (3) csomópont illeszkedik.
A hálózat alapegyenleteinek, a Kirchhoff egyenleteknek felírásához vonatkozási irányokat kell felvennünk. Ha ezen vonatkozási irányokat a hálózat gráfjának ágaihoz is hozzárendeljük, irányított gráfot kapunk (1.1 c. ábra).
Az olyan csomópont, amely csak egyetlen ághoz illeszkedik: végcsúcs és végcsúcshoz illeszkedő ág neve: végelem.
Általában az ághoz tartozónak tekintjük az ághoz illeszkedő két csomópontot is. A csomópont nélküli ágat megkülönböztetésül nyitott ágnak hívjuk.
Az olyan csomópont, amely nem illeszkedik egyetlen ághoz sem, izolált csomópont. Vissza
Tartalom
1. GRÁFELMÉLETI ALAPFOGALMAK 51.1 Gráfok és részgráfok 5
1.1.1 Út 8
1.1.2 Hurok 10
1.1.3 Fa és erdő 10
1.1.4 Vágat . 15
1.1.5 Csomópont 18
1.1.6 Fundamentális vágatrendszer 18
1.1.7 Fundamentális hurokrendszer 23
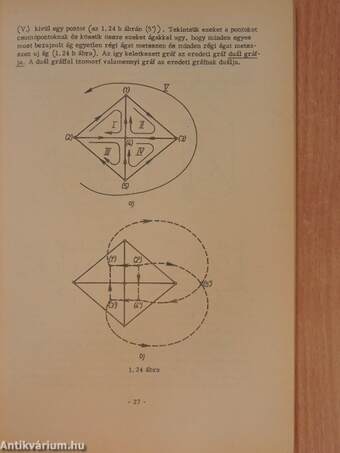
1.2 Izomorf és duál gráfok 25
1.2.1 Példa 30
1.3 A hálózat-mátrixok 33
1.3.1 Csomóponti mátrix 33
1.3.2 Hurokmátrix 35
1.3.3 Vágatmátrix 40
1.3.4 A hálózat-mátrixok közötti kapcsolatok 44
1.3.5 Példa 46
2. FESZÜLTSÉGEK ÉS ÁRAMOK MEGHATÁROZÁSA HÁLÓZAT-MÁTRIXOK FELHASZNÁLÁSÁVAL 51
2.1 Ohm-törvény 51
2.2 A Kirchhoff-törvények 58
2.3 Az ágáramok és ágfeszültségek.meghatározása 59
2.4 A faágak feszültségének és kötőágak áramának meghatározása 64
2.5 Példák és feladatok 66
2.6 A hurokáramok módszere 70
2.6.1 Példák és feladatok 72
2.7 A vágatfeszültségek módszere 77
2.7.1 Példa 79
2.8 A csomóponti potenciálok módszere 82
2.8.1 Feladatok 83
2.9 A dualitás elve 85
3. HÁLÓZATJELLEMZŐK MEGHATÁROZÁSA 89
3.1 Az n-pólus jellemzőinek számítása 89
3.1.1 A bemeneti impedancia és admittancia mátrix meghatározása 90
3.1.2 Generátort tartalmazó n-pólus jellemzőinek meghatározása 94
3.1.3 Példák és feladatok 95
3.2 m x n-pólus 201
3.2.1 Az admittancia és impedancia paraméter mátrix meghatározása 103
3.2.2 Generátort tartalmazó mxn-pólus jellemzőinek számítása 108
3.2.3 Feladatok 110
3.3 Átviteli mátrix 113
3.3.1 Hurokimpedancia mátrix alkalmazása 114
3.3.2 Vágatadmittancia mátrix alkalmazása 116
3.3.3 Példák és feladatok 119
4. SZÁMÍTÁS NULLÁTOROK ÉS NORÁTOROK FELHASZNÁLÁSÁVAL 123
4.1 A nullátor és a norátor 123
4.2 Csatolt kétpólusok és hálózati modelljük 125
4.3 Nullátort és norátort tartalmazó hálózat számítása 130
4.4 Példák 134
5. ÁLLAPOTEGYENLETEK 140
5.1 Az állapotváltozók kiválasztása 142
5.2 Az állapotegyenlet felírása 142
5.2.1 Példa 147
5.3 Az állapotegyenlet megoldása 150
5.3.1 Példa 155
IRODALOMJEGYZÉK 160
Megvásárolható példányok
Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.
Folytatás Microsoft-tal