Számolóábrák

Szerző

Lektor

Budapest

'Tuczy Tibor: Számolóábrák ' összes példány

Kiadó:	Műszaki Könyvkiadó
Kiadás helye:	Budapest
Kiadás éve:	1963
Kötés típusa:	Fűzött papírkötés
Oldalszám:	184 oldal
Sorozatcím:
Kötetszám:
Nyelv:	Magyar
Méret:	24 cm x 17 cm
ISBN:
Megjegyzés:	109 fekete-fehér ábrával illusztrálva.

Értesítőt kérek a kiadóról

A beállítást mentettük,
naponta értesítjük a beérkező friss
kiadványokról

Tartalom

Előszó	5
Általános ismertetés	7
Skálák	12
A lineáris skálák	12
A reciprok skálák	15
A hatványos skálák	16
A gyökös skálák	18
A hatványos-gyökös skálák	19
A negatív kitevőjű hatványos skálák	20
Tiszta számolási eljárás	20
Szerkesztés	21
A szinuszos és koszinuszos skálák	21
Megoldás táblázattal	22
Szerkesztés	23
A tangens és kotangens skálák	24
Megoldás táblázattal	25
Szerkesztés	26
A logaritmikus skálák	27
A lineáris függvények logaritmikus skálája	28
A reciprok függvények logaritmikus skálája	28
A hatvány logaritmusának skálája	28
A gyök logaritmusának skálája	30
Hatványos-gyökös függvény logaritmikus skálája	30
Negatív kitevőjű hatványfüggvény logaritmikus skálája	31
A szinusz és a koszinusz függvények logaritmált alakjának skálája	32
A tangens és a kotangens függvények logaritmált alakjának skálája	33
Az exponenciális függvények logaritmikus skálája	34
A logaritmus logaritmusának skálája	35
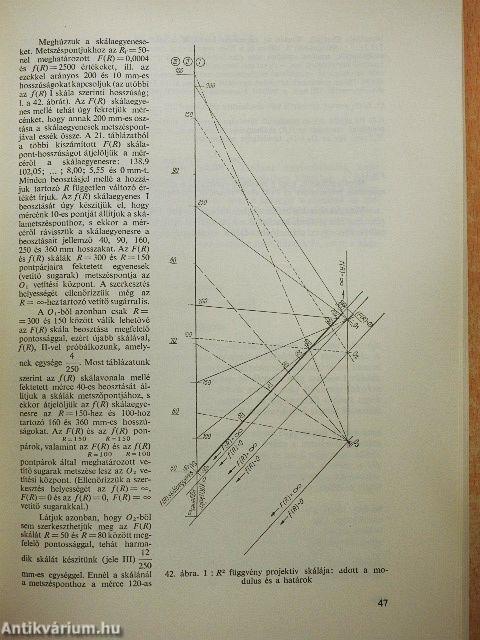
A projektív skálák	36
A projektivitás alaptulajdonságai	36
Példa	38
A kiindulási adatok változtatásának hatása a projektív skála szerkesztésének pontosságára	39
A vetítési központ áthelyezése	40
A skála egységének szerepe	40
A skálák metszéspontja eltolásának hatása	41
Az f(x) skála elforgatása	42
Számolóábrák	49
Skálasor	49
Értelmezés	49
Példák	50
Példa kísérleti eredmények ábrázolására	51
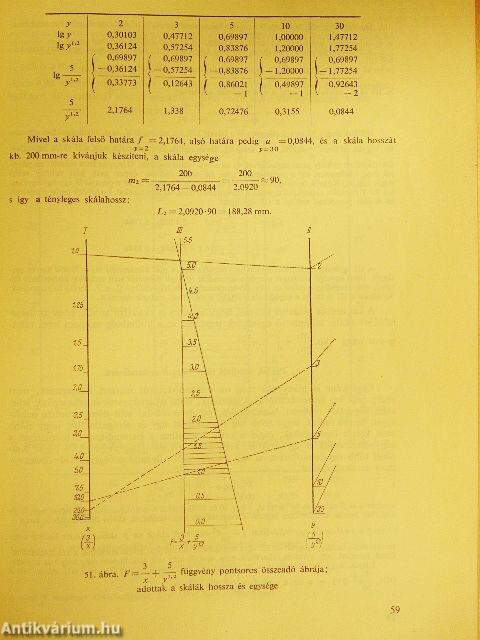
Pontsoros összeadóábra (Pö)	53
Példák két változó összeadására	55
Példák kettőnél több változó összeadására	60
Néhány tanács pontsoros ábra készítéséhez	63
Vonalsereges összeadóábra (Dö)	64
Példák	65
A Pö és a Dö ábrák összehasonlítása	68
A Z alakú szorzóábra	70
A V alakú szorzóábra	71
Hengeres test köbtartalmának kiszámítása a négy eljárással	72
A négyféle szorzóábra összehasonlítása	80
A skálahatárok növelése 10n szorzásával	81
Példa Z ábrára	81
Példa V ábrára	83
Szorzatból álló közös tényezőjű függvények együttes ábrája	85
Többtényezős szorzatok (és hányadosok) ábrái	87
V ábrák sorozatos kapcsolása	93
Megoldás Z és V ábrával	95
A logaritmikus skálájú Kü ábra	96
Az arányábra	97
A +Z ábra	98
Az X ábra	98
Az (x+y)v=u megoldása mindkét módszerrel	99
Példa Pöll ábrára	105
Megoldás Döll ábrával	106
Megoldás Zl ábrával	107
Megoldás Vl ábrával	107
Eltolható skálájú ábrák	122
A Descartes-féle derékszögű párhuzamos koordináta rendszeren alapuló számolóábrák	124
Függvények átalakítása, hogy a velük kapcsolatos feladatokat számolóábrával oldhassuk meg	126
A különböző elveken alapuló számolóábrák kapcsolásának lehetősége és módja	129
Grafikus számolás nem-kapcsolható ábrákkal	134
E könyv kereteit meghaladó számolóábrák	135
Függvények táblázata útmutatással számolóábrájuk megszerkesztésére	136