1.067.081
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát

VISSZA
A TETEJÉRE
JAVASLATOKÉszre-
vételek
A differenciál- és integrálszámítás elemei I. (töredék)
A Magyar Tudományos Akadémia támogatásával
| Kiadó: | Franklin-Társulat |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Könyvkötői vászonkötés |
| Oldalszám: | 476 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 25 cm x 17 cm |
| ISBN: | |
| Megjegyzés: | Töredék kötet. fekete-fehér ábrákkal illusztrált. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Tartalom
| Számsorozatok határértéke. Irracionális számok. | |
| Bevezetés | 1 |
| Példák monoton sorozatok határértékére | |
| A Bernoulli-féle egyenlőtlenség | 1 |
| A harmonikus sor divergenciája | 5 |
| Példák | 7 |
| A határérték fogalmának kiterjesztése tetszőleges sorozatra | |
| A véges határérték definiciója. Folyományok | 14 |
| A határértékkel bíró sorozat származtatása monoton sorozatból | 17 |
| A végtelen mint határérték | 20 |
| Zérus-sorozatok | |
| A zérus-sorozat definiciója | 21 |
| Összeg, szorzat és hányados határértéke | |
| Összeg határértéke | 28 |
| Szorzat határértéke | 29 |
| Hányados határértéke | 30 |
| Példa | 31 |
| Az n racionális tört kifejezésének határértéke | 33 |
| Szabályos sorozatok | |
| Példák racionális határértékkel nem bíró korlátos monoton sorozatokra | 34 |
| Szabályos sorozat | 37 |
| Szabályos sorozat tagjainak előjele | 40 |
| Euklidesi algoritmus. Incommensurabilis egyenesdarabok | 42 |
| Közönséges végtelen lánctört közelítő törtjeinek sorozata | 48 |
| Az irracionális számok bevezetése | |
| Szabályos sorozatok osztályai | 52 |
| A sorozat-osztályok aritmetikája. Valós számok | 56 |
| Valós tagú szabályos sorozatnak van határértéke | 68 |
| Az e szám | 69 |
| Végtelen tizedestört | 71 |
| Pozitív szám n-edik gyöke | 73 |
| Irracionális szám lánctört-kifejtése | 75 |
| Egyesesdarabok mérése. Példák | 79 |
| A számegyenes | 84 |
| Példák valós tagú sorozatok határértékére | |
| Példák | 87 |
| A Cauchy-féle határértéktételek | |
| Példa | 94 |
| Elemi függvények | |
| A kör kerülete | |
| A kör kerületének definiciója | 99 |
| A kerület mint felső, ill. alsó határ | 103 |
| A pí szám | 104 |
| Archimedes számításának ismertetése | 105 |
| Isoperimetrikus módszer 1/pí kiszámítására | 107 |
| Körív ívhosszúsága. Szög abszolút mérőszáma | 110 |
| Trigonometrikus függvények | |
| Adott abszolút mérőszámú szög létezése | 111 |
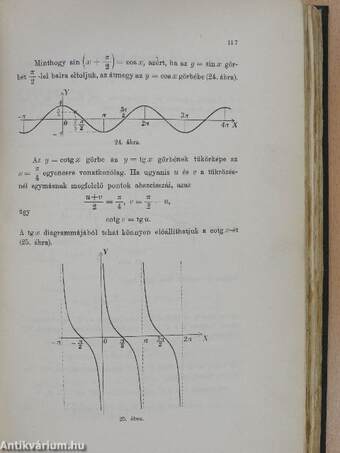
| Goniometriai formulák | 118 |
| A trigonometrikus függvények folytonossága | 119 |
| Két határérték | 130 |
| Tételek a beírt, ill. körülírt szabályos sokszögek kerületéről | 138 |
| Trigonometrikus összegképletek | 141 |
| Ciklometrikus függvények | |
| A logaritmus és az exponenciális függvény | |
| Adott modulusú logaritmus definiciója | 167 |
| A geometriai közép kisebb a számtani középnél | 184 |
| Másodfokú racionális egész függvény | |
| Másodfokú egyenlet | 196 |
| Lineáris törtfüggvény | |
| Az általános függvényfogalom | |
| A függvény általános definiciója | |
| A függvény általános definiciója | 212 |
| Függvények határértéke | |
| A határérték definiciója. Összeg, szorzat, hányados határértéke | 213 |
| Példák | 215 |
| Jobb- és baloldali határérték. Példák | 217 |
| A véges jobboldali határérték létezésének kritériuma | 218 |
| Függvények folytonossága | |
| A folytonosság definiciója. Különböző szakadási helyek | 223 |
| Példák | 225 |
| A folytonos függvények alaptulajdonságai | |
| Egyenletes folytonosság | 228 |
| Weierstrass tétele | 230 |
| Bolzano tétele | 231 |
| Valós együtthatós páratlanfokú egyenlet | 234 |
| A Kepler-féle egyenlet | 234 |
| Függvényegyenletek | |
| A differenciálhányados | |
| A differenciálhányados definiciója. Érintő | 240 |
| A differenciálható függvény folytonossága | 242 |
| Példa véges intervallumban végtelen sok helyen nem differenciálható folytonos függvényre | 243 |
| Jobb- és baloldali differenciálhányados. Végtelen differenciálhányados | 245 |
| Általános differenciálási szabályok | |
| Összeg és szorzat differenciálhányadosa | 246 |
| Determináns differenciálhányadosa | 247 |
| Hányados differenciálhányadosa | 248 |
| Közvetett függvény folytonossága és differenciálhányadosa | 249 |
| Logaritmikus differenciálhányados | 254 |
| Hiperbolás függvények | 255 |
| Invert függvény | 259 |
| A hiperbolás függvények inverzei | 262 |
| Kidolgozatlan példák | 265 |
| Példák határértékek meghatározására | 267 |
| A geometriai sor differenciálása | 268 |
| Érintő-szerkesztések | |
| Az érintő és a normális egyenlete. Subtangens és subnormális | 268 |
| Az ellipszis érintője | 271 |
| A cisszoid érintője | 272 |
| Parameteres előállítású görbék | 274 |
| A cyclois görbe | 277 |
| Polárkoordinátákban kifejezett egyenletű görbék. Spirálisok | 279 |
| Magasabbrendű differenciálhányadosok | |
| Magasabbrendű differenciálhányadosok szukcesszív képezése. Példák | 283 |
| Példák | 284 |
| A Leibniz-féle differenciálási szabály | 287 |
| Laguerre- és Legendre-polinomok | 287 |
| A differenciálható függvények alaptulajdonságai | |
| Adott helyen növekedő vagy fogyó függvény | |
| Növekedés, ill. fogyás adott helyen. A differenciálhányados előjelének szerepe | 289 |
| Növekedő, de nem monoton növekedő függvény | 290 |
| A differenciálhányados eltűnése belső extremális helyen | 290 |
| Darboux tétele | |
| Darboux tétele | 291 |
| Rolle tétele | |
| Rolle tétele véges intervallumra | 292 |
| Rolle tétele végtelen intervallumra | 293 |
| Waring tétele | 294 |
| A Lagrange-féle középértéktétel | |
| A Lagrange-féle középértéktétel és folyományai | 295 |
| Az egyszerű és a csillapított rezgőmozgás differenciálegyenlete | |
| Maximum-minimum feladatok | |
| Példák | 312 |
| A leggyorsabb érkezés elve a fénytörésnél | 317 |
| Minimális deviáció a prizmánál | 320 |
| Görbék alakja | |
| Konvexitás és konkávitás | 325 |
| A konvexitás, ill. konkávitás feltétele | 327 |
| Helyi szélsőérték. Inflexiós pont. | |
| Helyi maximum és minimum | 328 |
| Helyi minimum lehet a nélkül, hogy a függvény fogyóból növekedőbe menne át | 329 |
| Inflexiós pont | 330 |
| Függvények diszkussziója | |
| Általános eljárás függvények diszkussziójára | 331 |
| Példák | 332 |
| Kidolgozatlan példák | 354 |
| Aszimptota | |
| Az aszimptota fogalma, létezésének feltétele. Példák | 354 |
| Konvex vagy konkáv görbe aszimptotája | 358 |
| Példa | 362 |
| Függvények nagyságrendje | |
| A zérussá vagy végtelenné válás rendszáma | 364 |
| A függvény nagyságrendje többszörös 0-helyen | 365 |
| Alkalmazás határértékek meghatározására | 368 |
| Görbék érintkezése | |
| Az érintkezés rendszáma, különböző érintkezések | 369 |
| A görbe és az érintő érintkezése | 370 |
| Görbületi kör | |
| Görbületi kör | 373 |
| Példák | 375 |
| A görbületi sugár szélsőértékének esete | 380 |
| A görbületi középpont, mint két normális metszéspontjának határhelyzete | 381 |
| A görbületi középpont, mint a görbe három pontján átmenő kör középpontjának határhelyzete | 382 |
| Parameteres előállítású görbék görbületi sugara. Alkalmazás a cycloisra | 384 |
| A Cauchy-féle középértéktétel | |
| A Cauchy-féle középértéktétel | 386 |
| A L'Hospital szabály | |
| Hányados határértéke, midőn számláló és nevező 0-hoz tart | 388 |
| Példák | 389 |
| Hányados határértéke, midőn számláló és nevező abszolút értékben +végtelenhez tart | 391 |
| Példa | 393 |
| Kidolgozatlan példák | 395 |
| Racionális és trigonometrikus polinomok | |
| Racionális egész függvény gyökeinek multiplicitása | |
| Többszörös gyökök | 396 |
| A Legendre-, Laguerre- és Hermite-polinomok gyökei | 399 |
| Bizonyos számú helyen váltakozó előjelű polinom fokszáma | 401 |
| Bolzano és Rolle tétele racionális egész függvény esetében | |
| Bolzano tétele | 402 |
| Rolle tétele | 403 |
| Parabolikus interpoláció | |
| A Lagrange-féle interpolációs formula | 405 |
| A Taylor-formula | 407 |
| Hermite-féle interpoláció | 409 |
| A Newton-féle interpolációs formula. Osztott differenciák | 416 |
| Magasabbrendű differenciák. Aequidistans interpoláció | 419 |
| Rolle tételének általánosítása | 420 |
| A Schwarz - Stieltjes-tétel. Az osztott differenciák határértéke | 421 |
| A Lagrange-féle interpolációs formula maradéktagja | 425 |
| A Hermite-féle interpolációs formula maradéktagja | 431 |
| Csebisev-polinomok | |
| A Lagrange-féle interpolációs formula Csebisev-abszcisszák esetén | 438 |
| Racionális polinom átrendezése. Trigonometrikus összegképletek | 441 |
| Trigonometrikus polinomok | |
| Trigonometrikus polinom | 444 |
| A trigonometrikus polinomok alaptulajdonsága | 445 |
| Aequidistans trigonometrikus interpoláció | 446 |
| Interpoláció sinus-polinommal | 448 |
| Interpoláció cosinus-polinommal | 450 |
| Trigonometrikus polinom abszolút tagjának korlátai | 452 |
| Trigonometrikus polinom gyökeinek száma | 453 |
| Fejér tétele a trigonometrikus polinom magasságáról és mélységéről | 457 |
| Bernstein és Markov tétele | |
| Bernstein tétele n-edrendű trigonometrikus polinom differenciálhányadosána maximumáról | 463 |
| Markov tétele n-edfokú racionális polinom differenciálhányadosának maximumáról | 467 |
| Weierstrass approximáció-tétel | |
| Weierstrass első approximáció-tétele | 469 |
| Weierstrass második approximáció-tétele | 473 |
Megvásárolható példányok
Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.