Statisztikai módszerek a szerkezetek mechanikájában

Szerző

V. V. Bolotin

Fordító

Dr. Pomázi Lajos

Lektor

Dr. Körmendi István

Budapest

'V. V. Bolotin: Statisztikai módszerek a szerkezetek mechanikájában ' összes példány

Kiadó:	Műszaki Könyvkiadó
Kiadás helye:	Budapest
Kiadás éve:	1970
Kötés típusa:	Fűzött keménykötés
Oldalszám:	291 oldal
Sorozatcím:
Kötetszám:
Nyelv:	Magyar
Méret:	20 cm x 15 cm
ISBN:
Megjegyzés:	124 fekete-fehér ábrával illusztrálva. Tankönyvi szám: 10821.

Értesítőt kérek a kiadóról

A beállítást mentettük,
naponta értesítjük a beérkező friss
kiadványokról

Tartalom

Előszó a magyar kiadáshoz	9
Előszó	11
Bevezetés	13
A valószínűségelmélet és a matematikai statisztika elemei
A valószínűség értelmezése	20
A valószínűségelmélet néhány alaptétele	21
Példák	23
Valószínűségi változók és eloszlásuk jellemzői	25
Középértékek, momentumok és szórások	27
Normális eloszlás	29
Több valószínűségi változó együttes eloszlása	31
Több valószínűségi változó együttes eloszlásának számszerű jellemzői	33
Valószínűségi változók függvényei	35
Példa. A Rayleigh-eloszlás levezetése	37
Normális eloszlású változók lineáris transzformációja	38
Valószínűségi változók extremumainak eloszlása	41
Pearson-eloszlás	44
A matematikai statisztika tárgya. Empirikus eloszlások és azok legfontosabb jellemzői	46
Az empírikus és elméleti eloszlások közelségének becslése	48
Számítási előírások megalapozásának statisztikai módszerei
Bevezető megjegyzések	51
Általános helyzetkép	54
A statisztikai megfogalmazás egyéb változatai	55
Az anyagok szilárdságának empirikus eloszlásai	58
A terhelés empirikus eloszlásai	59
A törésmentesség garanciája N. Sz. Sztreleckij szerint	63
A törés valószínűsége A. R. Rzsanyicin szerint	64
Rúdszerkezetek törésének valószínűsége	67
A szerkezetek mechanikája és a megbízhatóságelmélet	67
Az előírt megbízhatóság meghatározása	71
A statisztikai módszerek és az építmények előírás szerinti számítása	74
A törés statisztikai elméletei
Előzetes megjegyzések	77
A ridegtörés statisztikai elmélete	79
A léptéktényező ridegtörés esetén	82
A szilárdság változékonysága rideg törésnél	84
A ridegtörési elmélet alkalmazása az építőanyagok szilárdságának vizsgálatára	92
A ridegtörési elmélet általánosítása, a hibák egyenlőtlen eloszlásának figyelembevétele	96
A fáradttörés statisztikai elméletei, a fáradttörés mint Markov-típusú sztochasztikus folyamat	102
A kifáradási határ statisztikai elmélete	104
A kifáradási görbe statisztikai elmélete	106
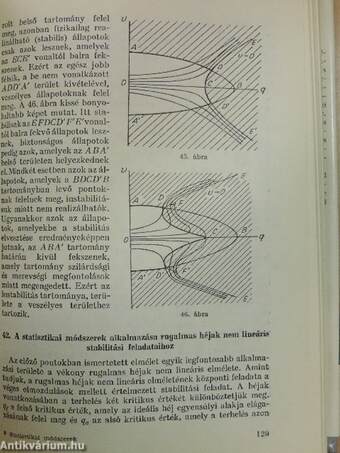
A statisztikai módszerek alkalmazása stabilitási feladatokhoz
A szerkezetek mechanikájában értelmezett stabilitás-fogalmak analízise	112
A véletlen zavarások figyelembevételéről	115
Néhány általános meggondolás	119
Példa. Véletlen kezdeti görbületű rúd hosszirányú hajlítása	122
Kritikus terhelések valószínűségeloszlásai	124
A veszélyes állapot valószínűségének meghatározása	127
A statisztikai módszerek alkalmazása rugalmas héja nem lineáris stabilitási feladataihoz	129
Lapos, hengeres héj	131
A statisztikai módszer héjakra vonatkozó további felhasználása	138
Befejezés, néhány dinamikai feladat	140
Szerkezetek rezgése véletlen erők hatására
Előzetes megjegyzések	144
Sztochasztikus folyamatok és jellemzőik	145
Stacionárius sztochasztikus folyamatok	148
A statisztikai dinamika módszereire vonatkozó általános megjegyzések	149
A stacionárius sztochasztikus folyamatok leírásának spektrális módszere	150
Véletlen hatások a legegyszerűbb lineáris rendszerre	153
Rugalmas rendszer lengése sztochasztikus hatások esetén	156
Feltételek, amelyek mellett az általánosított koordináták kölcsönös korrelációjától el lehet tekinteni	161
Térben-időben sztochasztikus terhelés-folyamat	163
Integrál-becslési módszer széles spektrumú terhelések esetére	166
Az Integrál-módszer néhány alkalmazás	173
Megoszló rendszerekk vizsgálatának korrelációs módszerei	183
Fokker-Planek-Kolmogorov egyenlete véletlen erőhatásoknak kitett rugalmas rendszer esetében	184
Néhány valószínűségeloszlásról	187
A bevezetett korlátozások mechanikai értelme	190
Néhány, a spektrális módszer segítségével megoldható statisztikai feladat	194
A károsodások felhalmozódása és a megbízhatóság becslése véletlen terhelések esetén
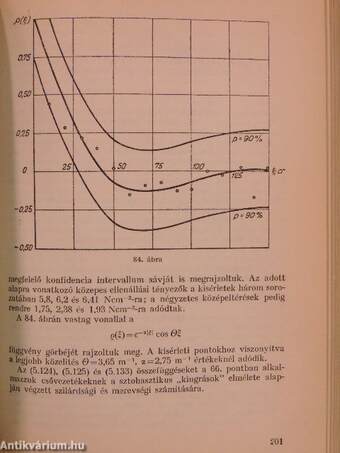
A probléma általános jellemzése	202
Adott szint túllépésének közepes száma sztochasztikus folyamatokban	205
A véletlen túlterhelések eloszlásának elméleti törvényei	207
Az építményre ható véletlen terhelések kombinációjára vonatkozó feladat	209
A véletlen túlterhelések eloszlástörvényének alkalmazása csővezetékek szilárdságának és merevségének becslésére	215
Maradó alakváltozások felhalmozódása véletlen túlterhelések során	217
A kifáradási károsodások felhalmozódása, a károsodások összegezésének elmélete és annak elemzése	222
A károsodások összegezési elméletének alkalmazása a szerkezetek élettartamának becslésére	226
A károsodások összegezési elméletének általánosítása	233
A fáradttörés két szakaszának elmélete	237
A fáradttörés két szakasza elméletének alkalmazás, összevetés a károsodások összegezési elméletével	240
Az élettartam becslése kvázistacionárius, sztohasztikus feszültségfolyamatok esetén	243
Kifáradási károsodások felhalmozódása széles sávú sztohasztikus folyamatot képző feszültségek esetén	247
Az élettartam alsó becslései széle sávú sztohasztikus folyamat esetén	252
A mechanikai tulajdonságok változékonyságának hatása az összesített élettartamra	257
A földrengésállóság elméletének statisztikai módszerei
Általános megjegyzések	259
A szeizmikus hatás instacionárius sztohasztikus folyamatként való előállítása	260
Példa	266
A sok komponensű szeizmikus hatás esete	271
A tönkremenetel és a várható élettartam valószínűségének becslése	274
A földrengés paramétereinek eloszlásfüggvényeiről	279
Az elmélet néhány gyakorlati vonatkozása	280
Irodalomjegyzék	282

Témakörök

Természettudomány > Fizika > Mechanika
Természettudomány > Matematika > Statisztika

V. V. Bolotin

V. V. Bolotin műveinek az Antikvarium.hu-n kapható vagy előjegyezhető listáját itt tekintheti meg: V. V. Bolotin könyvek, művek

Megvásárolható példányok

Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.

Előjegyzem