Statisztika

Matematikai statisztikai segédlet/Kézirat.

Szerző

Budapest

'Dr. Várlaki Péter: Statisztika ' összes példány

Kiadó:	Tankönyvkiadó
Kiadás helye:	Budapest
Kiadás éve:	1982
Kötés típusa:	Ragasztott papírkötés
Oldalszám:	350 oldal
Sorozatcím:
Kötetszám:
Nyelv:	Magyar
Méret:	24 cm x 17 cm
ISBN:
Megjegyzés:	Kézirat. Tankönyvi szám: J7-1009. Fekete-fehér ábrákat tartalmaz. Megjelent 535 példányban.

Értesítőt kérek a kiadóról

A beállítást mentettük,
naponta értesítjük a beérkező friss
kiadványokról

Előszó

A jegyzet célja az, hogy újszerű módon segítse a Közlekedésmérnöki Karon, a nappali és levelező tagozaton, továbbá a Gazdaságmérnöki Szakon a "Statisztika" című tantárgy anyagának elsajátítását.... Tovább

Tartalom

Bevezetés	3
Statisztikai minták	5
A statisztikai analízis és a statisztikai sokaság fogalma	5
A statisztikai analízis fogalma és alkalmazása	5
A statisztikai sokaság fogalma és jellemzése	6
Alapvető általános statisztikai módszerek	7
Statisztikai sorok és hisztogramok	7
Statisztikai középértékek	9
A szóródás mérőszámai	16
A statisztikai minta és a reprezentatív módszer elmélete	20
A statisztikai minta fogalma	20
A statisztikai minta eloszlása	21
A statisztikai minta eloszlásának alapvető paraméterei	23
Mintavétel véges sokaságból	27
A mintavétel főbb módszerei	30
Programozott gyakorlatok	35
A statisztikai analízis és a statisztikai sokaság	35
A sokaság centrumának jellemzése	37
A sokaság szétszóródásának jellemzése	47
A statisztikai minta és a mintavétel	55
Szakirodalom az 1. fejezethez	66
Ellenőrző kérdések az 1. fejezethez	67
Statisztikai becslések	69
A becsléselmélet elemei (A becslésekkel szemben támasztott követelmények)	69
Általános megjegyzések	69
A becslés torzítatlansága	70
A becslés hatékonysága és konzisztenciája	71
A becslés elégségessége	75
Becslési módszerek	76
A maximum-likelihood becslési módszer	76
Maximum-likelihood becslés többváltozós esetben	80
Bayes típusú becslések	82
A Bayes módszer alkalmazása valószínűségek becslésére: (a-priori és a-posteriori) szubjektív valószínűségek	92
A legkisebb négyzetek becslési módszere	95
Kapcsolat a különböző becslési módszerek között	99
Becslés sztochasztikus approximációval	100
Intervallumbecslések: konfidencia (megbízhatósági) intervallumok	105
Általános megjegyzések	105
Intervallumbecslések (konfidencia intervallumok) normális eloszlású eloszlású statisztikai sokaság m várható értékére ismert szórás esetén	106
Intervallumbecslés két normális eloszlású statisztikai sokaság várható értékeinek eltérésére, megegyező, de ismeretlen alapsokasági szórások esetén	110
Programozott gyakorlatok	112
Becsléselmélet elemei: konfidencia intervallumok	112
Becslési módszerek	122
Szakirodalom a 2. fejezethez	132
Ellenőrző kérdések a 2. fejezethez	133
Statisztikai hipotézisek	135
Általános problémafelvetés és hipotézisvizsgálati megközelítések	135
Szignifikancia vizsgálatok (Paraméteres és nemparaméteres próbák)	137
Általános megjegyzések	137
Paraméteres próbák (Várható értékekkel és szórásokkal kapcsolatos szignifikancia vizsgálatok)	139
Szekvenciális módszer hipotézisvizsgálatra	147
A nemparaméteres próbák (szignifikancia vizsgálatokra)	150
A x-próbák	153
Hipotézisvizsgálat a Neyman-Pearson kritérium alapján	157
Bayes tipusú próbák	158
Szóráselemzés	161
A többváltozós statisztikai elemzés további lehetőségei	165
Programozott gyakorlatok	167
Szakirodalom a 3. fejezethez	199
Ellenőrző kérdések a 3. fejezethez	200
A statisztikai összefüggések (korreláció és regresszió analízis)	201
Sztochaisztikus kapcsolatok, statisztikai függőségi mérőszámok	201
Kétváltozós statisztikai összefüggés vizsgálatok	202
A korrelációs együttható és a lineáris regresszió	202
A korrelációs együttható és a lineáris regresszió becslése	205
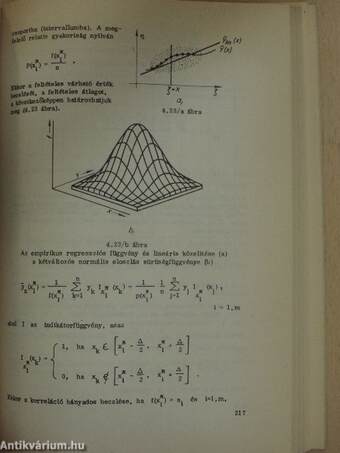
A korrelációs hányados és a feltételes várható érték	210
A korreláció hányados és a regressziós függvények becslése	216
A négyzetes kontingencia és függetlenségi vizsgálat	223
Többváltozós statisztikai kapcsolatok, függőségi mérőszámok. A többváltozós lineáris regresszió	226
A többváltozós lineáris regresszió	226
A parciális és többszörös korrelációs együttható	230
A töbváltozós regresszió becslése	234
A parciális és többszörös korrelációs együtthatók becslése	237
Programozott gyakorlatok	239
(Függelék:) A statisztikai analízis általános statisztikai döntéselméleti megfogalmazásának lehetősége	263
Szakirodalom a 4. fejezethez	267
Ellenőrző kérdések a 4. fejezethez	268
A véletlen (sztochasztikus) folyamatok (idősorok) statisztikája	269
Statisztikai minták véletlen folyamatokra	269
A véletlen (sztochasztikus) folyamatok értelmezése	269
A statisztikai minta értelmezése sztochasztikus folyamatokra	270
A vizsgált véletlen folyamatok tipizálása	275
Statisztikai hipotézisek véletlen folyamatokra	290
A statisztikai összefüggések vizsgálata véletlen folyamatokra	290
A statisztikai összefüggés vizsgálatok feladata	290
Előrebecslés, prognózis (extrapoláció) stacionárius folyamatokra (idősorokra)	291
Statisztikai identifikáció (modellépítés) lineáris dinamikus rendszerekre	293
Lineáris szűrők (filtráció)	300
Az idősorok statisztikája	302
Az idősor fogalma és összetevői	302
A trendösszetevők meghatározásának elemi megközelítései	303
Korszerű idősoranalízis autoregresszív és mozgóátlag típusú modellekkel (ARIMA módszer)	306
Az ARIMA idősor analízis módszer alkalmazása a lineáris rendszerek statisztikai identifikációjára	311
Több komponens együttes figyelembevétele, az idősorok spektrálanalízise	313
Programozott gyakorlatok	321
Szakirodalom az 5. fejezethez	342
Ellenőrző kérdések az 5. fejezethez	343
Általános statisztikai irodalom	345

Témakörök

Megvásárolható példányok

Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.

Előjegyzem