1.066.456
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát

VISSZA
A TETEJÉRE
JAVASLATOKÉszre-
vételek
Hidrológiai statisztika
Egyetemi tankönyv
| Kiadó: | Tankönyvkiadó Vállalat |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Fűzött kemény papírkötés |
| Oldalszám: | 519 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 24 cm x 17 cm |
| ISBN: | 963-17-6647-0 |
| Megjegyzés: | A könyv tankönyvi száma: 44463. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Tartalom
| Bevezetés | 11 |
| Valószínűségszámítási alapfogalmak | 17 |
| A valószínűség fogalma és szerepe a hidrológiában | 17 |
| A véletlen esemény fogalma | 17 |
| A valószínűség fogalma | 22 |
| Kombinatorikai alapok | 27 |
| Példák a valószínűségek kombinatorikus kiszámítására | 33 |
| Feltételes valószínűség és függetlenség | 37 |
| Valószínűségi változók és valószínűségeloszlások | 50 |
| A valószínűségi változó és valószínűségeloszlások fogalma | 50 |
| A valószínűségeloszlásokra vonatkozó általános ismeretek | 50 |
| A többdimenziós eloszlás fogalma | 59 |
| Feltételes eloszlás- és sűrűségfogalom | 62 |
| A valószínűségi változó monoton függvényének eloszlása | 67 |
| Két független valószínűségi változó összegének eloszlása | 67 |
| Két független valószínűségi változó szorzatának és hányadosának eloszlása | 69 |
| Valószínűségeolszlások jellemzői | 71 |
| A várható érték fogalma és tulajdonságai | 72 |
| A feltételes várható érték | 76 |
| A szórás fogalma és tulajdonságai | 78 |
| A valószínűségi változókm momentumai | 81 |
| A korrelációs együttható | 84 |
| A generátorfüggvény és a karakterisztikus függvény | 88 |
| A generátorfüggény | 88 |
| A karakterisztikus függvény | 89 |
| A fontosabb valószínűségeloszlások áttekintése | 92 |
| Diszkrét valószínűségeloszlások | 93 |
| Egyszerű alternatíva | 93 |
| A binomiális eloszlás | 94 |
| A polinomiális eloszlás | 101 |
| A geometriai eloszlás | 101 |
| A Poisson-eloszlás | 105 |
| Folytonos valószínűségeloszlások | 110 |
| A normális eloszlás | 110 |
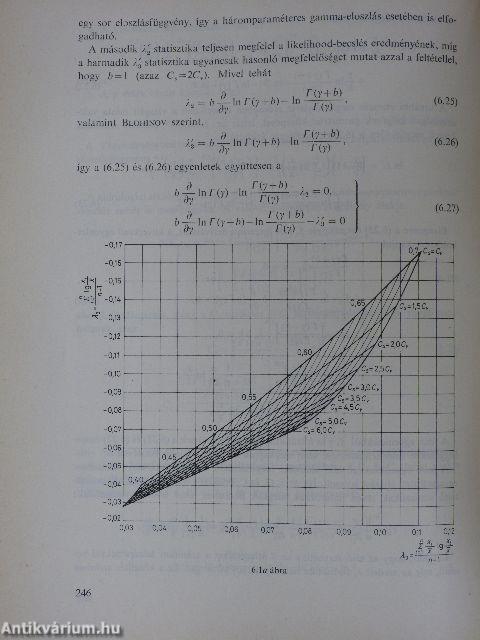
| A gamma-eloszlás | 131 |
| A nagy számok törvénye | 168 |
| A nagy számok törvényének Bernoulli-féle alakja | 168 |
| A centrális határeloszlát tétele | 171 |
| A matematikai statisztika és annak hidrológiai alkalmazásai | 176 |
| A hidrológiai statisztikai módszerek sajátosságai | 177 |
| A matematikai statisztika mint a valószínűségelmélet egy fejezete | 178 |
| A statisztikai minta | 181 |
| A statisztikai függvény | 183 |
| Az empirikus eloszlásfüggvény. Glivenko tétele | 185 |
| A legfontosabb empirikus jellemzők | 187 |
| A mintaközép | 187 |
| Az empirikus medián | 189 |
| Az empirikus kvantilisek | 189 |
| Az empirikus szórásnégyzet | 190 |
| A variációs tényező | 192 |
| Az aszimmetriatényező | 192 |
| A tapasztalati sűrűségfüggvény | 194 |
| A rendezett minták elméletének elemei | 203 |
| A rendezett minták fogalma | 203 |
| A rendezett mintaelemek eloszlása | 204 |
| A rendezett mintaelemek eloszlása exponenciális eloszlás esetén | 207 |
| A maximális túllépések eloszlásának meghatározása | 209 |
| A Kolmogorov-Szmirnov-típusú határeloszlások | 214 |
| Grafikus eloszlásvizsgálat | 218 |
| Valószínűségi hálózatok | 218 |
| Közelítő paraméterbecslések | 224 |
| Valószínűségi változók átalakítása | 230 |
| A bekövetkezési valószínűség és a tervezési kockázat | 232 |
| Statisztikai becsléselmélet | 236 |
| A becslés problémája | 236 |
| A becslés módszerei | 237 |
| A momentumok módszere | 238 |
| A maximum-likelihood-módszer | 240 |
| A becslés tulajdonságai | 248 |
| A becslés torzítatlansága | 248 |
| A becslés hatásfoka | 250 |
| Erősen konzisztens és konzisztens becslések | 252 |
| A Cramer-Rao-egyenlőtlenség | 253 |
| Elégtelen becslések | 256 |
| Intervallumbecslés. Megbízhatósági (konfidencia-) intervallumok | 259 |
| A normális eloszlás várható értékének konfidenciaintervalluma | 261 |
| A normális eloszlás szórásnégyzetének konfidenciaintervalluma | 262 |
| Az exponenciális eloszlás paraméterének konfidenciaintervalluma | 263 |
| Az árvízi vízállástúllépések empirikus eloszlásfüggvényének konfidenciaintervalluma | 266 |
| Statisztikai hipotézisek vizsgálata | 267 |
| A statisztikai hipotézisvizsgálat hidrológiai sajátosságai | 267 |
| Paraméteres és nem paraméteres problémák | 270 |
| A statisztikai próba | 270 |
| A próba erőfüggvénye | 274 |
| A statisztikai próbák általános tárgyalása | 277 |
| Paraméteres próbák | 278 |
| A Student-féle t-próba | 278 |
| A Welch-próba | 286 |
| Az F-próba | 287 |
| Több szórás megegyezésének vizsgálata; a Barlett-próba | 293 |
| A Pitman-próba | 294 |
| Több normális eloszlású valószínűségi változó várható értékének összehasonlítása (szórásanalízis) | 295 |
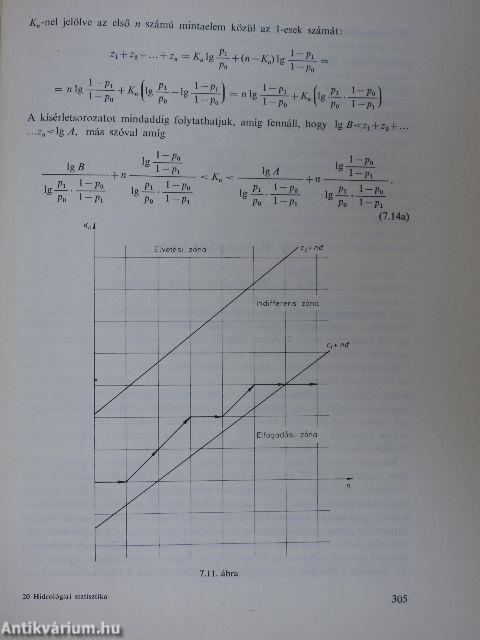
| Szekvenciális módszer hipotézisvizsgálata | 299 |
| Illeszkedésvizsgálat | 306 |
| Az illeszkedésvizsgálat feladatai | 306 |
| A x2-próba | 307 |
| A Kolmogorov-próba | 323 |
| Normalitásvizsgálat a mintaelemek transzformációja alapján (Sarkadi-próba) | 330 |
| Az exponenciális eloszlásra vonatkozó hipotézis vizsgálata (Störmer-próba) | 331 |
| Homogenitásvizsgálat | 332 |
| A homogenitásvizsgálat általános célkitűzései | 332 |
| A Wilcoxon-próba | 334 |
| Homogenitásvizsgálat kombinatorikus módszerrel | 338 |
| A Kolmogorov-Szmirnov-féle kétmintás próba | 342 |
| Néhány homogenitásvizsgálati módszer összehasonlítása | 344 |
| Véletlenségvizsgálat | 347 |
| A Wald-Wolfowitz-próba | 348 |
| Futampróbák alkalmazása | 350 |
| Események valószínűségére vonatkozó hipotézisek vizsgálata | 352 |
| A P(A)=p nullhipotézis ellenőrzése | 352 |
| A döntésfüggvények elméletének elemei | 354 |
| A statisztikai döntési eljárás | 355 |
| Veszteségfüggvény és kockázatfüggvény | 356 |
| A Bayes-féle döntési elv | 357 |
| Árvédekezési döntések | 361 |
| Korrelációanalízis | 365 |
| A sztochasztikus kapcsolatok jellemzése | 365 |
| A regressziós függvény | 368 |
| A korrelációs együttható statisztikai vizsgálata | 369 |
| Az indikátorkorreláció | 372 |
| Az indikátorkorreláció becslése | 376 |
| Függőségvizsgálat a kvantilisértékek segítségével | 380 |
| Valószínűségek közelítő kiszámítása kétdimenziós valószínűségeloszlások esetén | 381 |
| Extremális értékek sztochasztikus kapcsolata kétdimenziós eloszlások esetén | 386 |
| Információelméleti meggondolások valószínűségi változók közötti sztochasztikus kapcsolatok vizsgálatára | 388 |
| Árvízi vízállások sztochasztikus kapcsolatai | 395 |
| Regresszióanalízis | 398 |
| A legkisebb négyzetek módszere. A regressziós görbe | 398 |
| Regresszió kétváltozós normális eloszlás esetében | 399 |
| Lineáris regresszió becslése a statisztikai mintából | 401 |
| Két változó lineáris függvénykapcsolatának statisztikai vizsgálata | 411 |
| Regressziós felület és sík | 413 |
| Többváltozós lineáris függvénykapcsolat. A Gauss-féle normálegyenletek | 416 |
| Polinomiális regresszió | 423 |
| Parciális korreláció | 424 |
| Többszörös korreláció | 426 |
| Regresszióvizsgálat a kvantilisgörbével | 427 |
| A kvantilisgörbe alkalmazása árhullámok vizsgálatára | 433 |
| Több mérőállomás adatainak összevonása | 435 |
| Kapcsolatvizsgálat belső függést mutató adatsorok esetén | 437 |
| A sztochasztikus folyamatok elméletének elemei. Markov-láncok | 439 |
| A víz körforgása mint sztochasztikus folyamat | 439 |
| Markov-láncok. Markov-folyamatok | 445 |
| A Markov-lánc fogalma | 445 |
| Alkalmazási példák | 448 |
| Tározók kiürülési, ill. túlfolyási valószínűségeinek meghatározása | 453 |
| Hidrológiai idősorok ergodicitása | 461 |
| Korreláció a Markov-láncokban | 466 |
| Markov-lánc állapotai közötti függőség vizsgálata információelméleti eszközökkel | 468 |
| Összetett Markov-láncok | 471 |
| Véges vagy megszámlálhatóan végtelen sok állapotú Markov-folyamatok | 473 |
| Stacionárius folyamatok a hidrológiában | 476 |
| A stacionárius folyamatok jellege | 476 |
| Alkalmazási példák | 480 |
| Ergod-tétel stacionárius folyamatokra | 484 |
| Hidrológiai idősorok elemzésének néhány statisztikai módszere | 486 |
| Trendvizsgálat | 486 |
| Periódusvizsgálat | 488 |
| Autoregresszív modellek | 498 |
| Az átlagfüggvénytől való maximális eltérések vizsgálata | 508 |
| Irodalomjegyzék | 511 |
| Tárgymutató | 517 |
Megvásárolható példányok
Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.