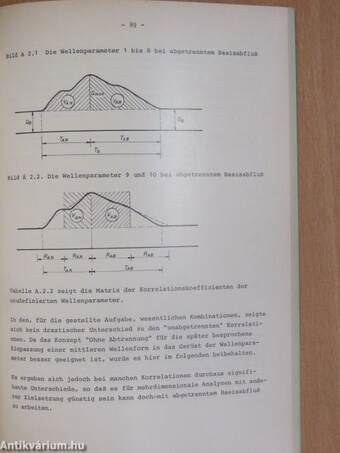
1.118.537
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát
Mitteilungen Heft 167.
Versuchsanstalt für Wasserbau und Kulturtechnik/Theodor-Rehbock-Flußbaulaboratorium/Universität Fridericiana Karlsruhe/Reports/Number 167/Research Institute for Hydraulic Structures and Agricultural Engineering/Theodor-Rehbock-Laboratory for River Improvement/University Fridericiana Karlsruhe/Communiqués/Fascicule 167/Institut de Recherches de Constructions Hydrauliques et Génie Rural/Laboratoire de Constructions Fluviaux Theodor Rehbock/Université Fridericiana de Karlsruhe
| Kiadó: | Theodor-Rehbock-Flußbaulaboratorium |
|---|---|
| Kiadás helye: | Karlsruhe |
| Kiadás éve: | |
| Kötés típusa: | Ragasztott papírkötés |
| Oldalszám: | 130 oldal |
| Sorozatcím: | Mitteilungen |
| Kötetszám: | 167 |
| Nyelv: | Német |
| Méret: | 20 cm x 15 cm |
| ISBN: | |
| Megjegyzés: | Fekete-fehér ábrákkal, kihajtható melléklettel. Angol és francia nyelvű tartalomjegyzékkel, összefoglalóval. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Előszó
Im vorliegenden Heft werden zwei Beiträge behandelt, die im Rahmen
von Dissertationen angefertigt wurden und thematisch in den Bereich
der Hydrologie einzuordnen sind. Insbesondere werden hier... Tovább
Előszó
Im vorliegenden Heft werden zwei Beiträge behandelt, die im Rahmen
von Dissertationen angefertigt wurden und thematisch in den Bereich
der Hydrologie einzuordnen sind. Insbesondere werden hier Probleme
der probabilistischen und stochastischen Hydrologie herausgegriffen
und in wissenschaftlicher Fragestellung näher beleuchtet.
Herr Dr.-Ing. Helmut Eggers, wissenschaftlicher Angestellter und
Lehrbeauftragter im Landwirtschaftlichen Wasserbau am Institut für
Wasserbau und Wasserwirtschaft der Universität Karlsruhe, behandelt
in seiner Dissertation (mdl. Prüfung am 1. Dezember 1975) den Ein-
fluß seltener Ereignisse bei der Bestimmung der Hochwasserwahrschein-
lichkeit. Es wird zunächst gezeigt, daß die schiefe Verteilung,
Typ III v.K. Pearson, für die Hochwasserabflüsse im Gebiet der Bundes-
republik Deutschland gut geeignet ist. Weiterhin stellt sich heraus,
daß die Unterschiede der Quantile bei Verwendung von Parameterschätz-
verfahren nach der "Maximum-Likelihood Methode" und der "Momenten-
methode" nur eine Größenordnung von rund 10% erreichen. Der Einfluß
von Ausreißern wird an der Pearson-Typ III Verteilung gezeigt, deren
Parameter über die Momentenmethode geschätzt werden. Dabei erweist
sich, daß die Schiefe einer Stichprobe mit Ausreißern nur abhängig
von der "Urschiefe" und der "Urstichprobengröße", sowie dem Wieder-
kehrintervall der Ausreißer ist. Zum Schluß wird gezeigt, von wel-
cher Größe die Quantilerhöhung infolge eines Ausreißers ist und wel-
che Entscheidungsprozedur möglich ist, ob ein verdächtig großer Stich-
probenwert als Ausreißer definiert und behandelt werden sollte.
Herr Dr.-Ing. Sepp Weingärtner, wissenschaftlicher Angestellter,
ebenfalls am Institut für Wasserbau und Wasserwirtschaft der Univer-
sität Karlsruhe, beschreibt in seiner Dissertation (mdl. Prüfung am
15. Juni 1976) ein neues stochastisches Modell zur Erzeugung von
Hochwasserwellen, über die bestehenden eindimensionalen Ansätze
hinaus entwickelt er ein zweidimensionales Modell zur Wellensyn-
these. Im einzelnen erzeugt das Modell das gemeinsame Auftreten von
Scheitel und Dauer der Welle. Die Simulation arbeitet dabei über die
bi-lognormale Dichtefunktion der gemeinsamen Wahrscheinlichkeit. Die
Scheitelanstiegszeit als dritte unabhängige Größe wird mit Hilfe Vissza
Tartalom
Seite
Teil I
H. Eggers
Der Einfluß seltener Ereignisse
bei der Bestimmung der
Hochwasserwahrscheinlichkeit 1-14 5
Teil II
S. Weingärtner
Statistisch erzeuqte Serien von
Hochwasserwellen
1-116
Témakörök
- Idegennyelv > Idegennyelvű könyvek > Német > Műszaki
- Idegennyelv > Idegennyelvű könyvek > Német > Egyéb
- Idegennyelv > Idegennyelvű könyvek > Német > Folyóiratok, újságok
- Folyóiratok, újságok > Műszaki
- Mezőgazdaság > Vízgazdálkodás > Általában
- Műszaki > Idegennyelv > Német
- Műszaki > Vízgazdálkodás
- Műszaki > Folyóiratok, közlemények > Egyéb
- Műszaki > Folyóiratok, közlemények > Idegennyelv