Mindenki matematikája

Szerző

Szerkesztő

Fordító

Lektor

Budapest

'R. Wesley: Mindenki matematikája ' összes példány

Kiadó:	Gondolat Kiadó
Kiadás helye:	Budapest
Kiadás éve:	1963
Kötés típusa:	Félvászon
Oldalszám:	604 oldal
Sorozatcím:
Kötetszám:
Nyelv:	Magyar
Méret:	20 cm x 15 cm
ISBN:
Megjegyzés:	Fekete-fehér ábrákkal illusztrálva.

Értesítőt kérek a kiadóról

A beállítást mentettük,
naponta értesítjük a beérkező friss
kiadványokról

Tartalom

Bevezetésül - egy kis magyarázat	5
Mi a matematika?	9
Hány nap van egy évben?	9
Gyakorlati matematika - iskolai matematika	15
A matematika nyelve	16
A geometria gyakorlati alapjai	20
Mivel foglalkozik az algebra?	23
Milyen hosszú a centiméter?	28
Közönséges és másfajta törtek	29
Számok és álokoskodások	30
A matematika nyelve	33
Aritmetika: itt számokkal dolgozunk	33
Munkáljuk meg kissé a törtek talaját!	33
A tizedes törtekkel könnyű bánni!	37
Százalékszámítás dióhéjban	42
Néhány szó a tízes- és az angol mértékrendszerről	43
A brit és a metrikus egységek átszámításának táblázata	45
Területszámítás	45
Néhány tudnivaló a körről	49
Néhány test felszínének képlete	51
A testek térfogatáról	52
A négyzetgyökök és a köbgyökök fogalmának rövid magyarázata	55
Az algebrai jelek segítségével időt takaríthatunk meg	57
Csináljunk mi is képleteket!	60
Képletek (egyszerű egyenletek) átalakítása	62
Egyszerű algebrai műveletek	65
Hogyan bánjunk a pozitív és negatív előjelekkel?	68
Az algebra felhasználása a szöveges feladatok megoldására	80
Egyenletrendszerek	84
Másodfokú egyenletek	86
Geometria: Vonalak, alakzatok és szögek	98
Mit kell tudnunk a szögekről?	99
Mikor párhuzamos két egyenes?	102
Beszéljünk a háromszögekről!	104
A vetítőgép geometriája	113
Próbálkozzunk meg egy kis gyakorlati munkával!	117
Másfajta geometriai alakzatok	120
A kör geometriája	124
Érintők és húrok	128
Trigonometria - mint a geometria továbbfejlesztésének terméke	131
A tangens szögfüggvény használata	136
A sinus és cosinus fogalmának felhasználása a gyakorlatban	140
És ha a háromszög nem derékszögű	146
90°-nál nagyobb szögek szögfüggvényei	151
Az erőparalelogramma	155
A szögek ívmértéke	158
A grafikonok a számokat képekben ábrázolják	159
A piktográfok értéke	161
Oszlopdiagramok	162
Pont- és vonalgrafikonok	164
Körcikk-diagramok	167
Folytonos egyenesekkel ábrázolható összefüggések	168
Görbevonalú grafikonok	176
Néhány gyakorlati példa	179
Harmadfokú és egyéb görbék	183
Milyen segítséget ad nekünk a differenciál- és integrálszámítás?	186
Az idő-változó	200
Az integrálszámítás	205
Mivel foglalkozik könyvünk a továbbiakban?	213
Néhány hasznos fogás	215
Miben segít bennünket a logaritmus táblázat?	219
Mi határozza meg a dobozok alakját?	223
Hogyan lehet jól gazdálkodni a kerítéssel?	229
Az utazás matematikája	235
Helyzetünk meghatározása	236
Hogyan határozzuk meg a földrajzi hosszúságot és szélességet?	241
Merre van észak?	249
A térképrajzolók problémái	254
A méretarány problémája	261
Mi a szerepe a földmérőnek a térképészetben?	264
A navigáció fejlődése	266
Az idő mérése	272
Napidő és csillagidő	274
A Gergely-féle naptár	277
A nap felosztása	278
Idő és földrajzi hosszúság	280
Egyre sebesebben	282
Az idő és az utazás problémái	283
Számok és alakzatok a természetben	295
A biológiában is szükség van mérésekre	296
A grafikonok és az algebrai ismeretek alkalmazása a biológiában	298
Az egyéni szervezetek növekedésének mértéke	310
Az egyéni változatok és a normális valószínűségi eloszlás görbéje	312
Mit értünk a valószínűség fogalmán?	321
A binomiális tétel felhasználása	324
A valószínűségi integrálok szerepe	333
A statisztikai mintaátlag szórása	334
A korreláció fogalma	336
Az átöröklés matematikája	339
Kísérletek a dihibrid átörökléssel kapcsolatban	347
A trihibrid átöröklés	350
Mendel munkásságának újra felfedezése és továbbfejlesztése	353
A nem meghatározása	356
Kapcsolódás, átkereszteződés és kromoszóma-térképek	358
A több-tényezős átöröklés	363
A geometria az élők világában	365
A testformák geometriája	373
Az építész és az amatőr kőműves matematikája	381
A tizenkettes számrendszer: az építészek számolási rendszere	388
Az alapozás fontossága	393
Az alapozás előkészítése és végrehajtása	396
A betonnal és a vakolattal kapcsolatos számítások	399
A víz és a cement aránya	401
A falak építésével kapcsolatos számítások	404
A téglaboltövek geometriája	411
Mikor használunk épületfát?	415
A fa nedvességtartalma és kiszárítása	417
Az ajtók és padlók vetemedése	421
Matematikai adalékok a tartókkal kapcsolatban	424
A fesztávolság hatása a lehajlásra	427
A házak fűtése és vízellátása	431
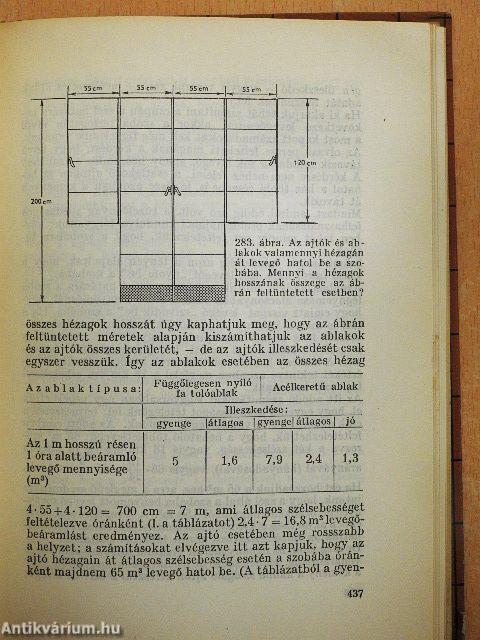
Az ajtók és ablakok okozta léghuzat	436
Hogyan zárja ki házunkból a tetőszerkezetet a hideget?	440
A lakás vízellátásáról	442
Számítások a primér áramlással kapcsolatban	448
A gázfogyasztás mérése	450
Egy kis népszerű mechanika	453
A tetőszerkezet megkötése	469
A folyadéknyomásról	471
A kerékpár és a gépkocsi	475
A változtatható áttételekről	478
Az áttételi arány megválasztása	482
Hogyan működik a kerékpár?	484
A pörgettyű-hatás	488
"Hogy tud! Nem is fogja a kormányt!"	490
A mozgást akadályozó erők	493
A munka és a teljesítmény	497
Milyen gyorsan haladhat a kerékpáros?	498
A gépjárművek teljesítményviszonyai	504
A villamosság matematikája	513
Ohm törvénye	516
Soros- és párhuzamos kapcsolás	518
A villanyszámla	521
Az izzólámpa fényessége	523
A feszültségesés	525
Feszültségesés a vezetékben	527
Az áram távvezetése	531
A wattnélküli áram, az impedancia fogalma	536
A maximális és az effektív feszültség	539
Háromfázisú áram vezetése	541
A váltakozó áram egyenirányítása	542
A rádió	544
A moduláció	546
Az elektroncső	547
Esélyek a játékosokban és a sportokban!	553
A rendszámtáblák számadatairól	556
A totó matematikája	560
A permutáció fogalma	562
A kombinációk fogalma	569
Példák a permutációkra és a kombinációkra	574
Néhány egyszerű számítás a bridzs esélyeivel kapcsolatban	577
Faites vos jeux!	584
Megoldások	590