1.067.053
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát

VISSZA
A TETEJÉRE
JAVASLATOKÉszre-
vételek
Mechanika
Általános szilárdságtan/Kézirat/Budapesti Műszaki Egyetem Építőmérnöki Kar
| Kiadó: | Tankönyvkiadó Vállalat |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Ragasztott papírkötés |
| Oldalszám: | 223 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 24 cm x 17 cm |
| ISBN: | |
| Megjegyzés: | Kézirat. 309 példányban jelent meg. Tankönyvi szám: J 9-1059. 72 fekete-fehér ábrával illusztrálva. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Előszó
E jegyzet az Építőmérnöki Kar Közlekedés-, Szerkezet- és Vízépítőszakos hallgatói részére készült és a Mechanika tárgy reformtanterv által megszabott általános szilárdságtan anyagát tartalmazza.A... Tovább
Előszó
E jegyzet az Építőmérnöki Kar Közlekedés-, Szerkezet- és Vízépítőszakos hallgatói részére készült és a Mechanika tárgy reformtanterv által megszabott általános szilárdságtan anyagát tartalmazza.A jegyzet szorosan kapcsolódik az 1975. évben megjelent "Elemi Szilárdságtan" című jegyzet anyagához, és feltételezi a matematika mátrix- és tenzor-aritmetikával, valamint a közönséges és parciális differenciálegyenletekkel kapcsolatos alapvető fogalmainak és tételeinek ismeretét.
A tárgyalt problémák matematikai leírásán túlmenően igen nagy gondot fordítottunk a fogalmak és összefüggések fizikai tartalmának alapos és sokoldalú megvilágítására. Reméljük, hogy ezek megértése és elsajátítása eredményesen hozzá fog járulni hallgatóink jó mérnöki érzékének és önálló gondolkodásának kialakításához.
Az anyag ismertetését megelőzően köszönetünket fejezzük ki a jegyzet lektorának, dr. Csellár Ödön docensnek, aki a kézirat szokásos, rutinszerű ellenőrzésén túlmenően sok értékes javaslattal segítette elő a feladatok tömörebb és pedagógiailag tökéletesebb tárgyalását. Az ábraanyag szakszerű elkészítése Tamássy Tamásné érdeme, a kézirat gondos legépelése pedig Kosinsky Judit munkáját dicséri.
Kívánjuk, hogy hallgatóink e jegyzetet örömmel és haszonnal tanulmányozzák. Vissza
Tartalom
1. BEVEZETÉS ......................................................111.1 Az általános szilárdságtan tárgya és felosztása ......11
1.2 Feltevések. A jegyzet felosztása..............................12
1.3 A jegyzet technikai kérdései ..................................13
2. A SZILÁRD TEST STATIKAI VIZSGÁLATA......................15
2.1 A feszültségállapot általános vizsgálata......................15
2.11 Feltevések, alapfogalmak ..............................15
2.12 A feszültségállapot fogalma ..............................17
2.13 A feszültségtenzor és a feszültségmátrix............18
2.131 A különböző metszetekhez tartozó feszültségvektorok meghatározása............18
2.132 A feszültségállapot mint tenzorfogalom ............23
2.2 A feszültségállapot vizsgálata a főfeszültségek segítségével ......................24
2.21 A főtengely-tétel. Főfeszültségek és feszültségi főirányok ...........24
2.22 A feszültségi ellipszoid. Speciális feszültségállapotok ...........................29
2.23 A síkbeli feszültségállapot.........................32
2.24 A feszültségi Mohr-körök..................................39
2.241 A feszültségi fősíkok törvényszerűségei ... 39
2.242 A Mohr-kör fogalma és tulajdonságai .... 39
2.243 Általános (térbeli)feszültségállapot ábrázolása Mohr-körökkel. Főnyírófeszültségek..............46
2.244 Különleges feszültségállapotok Mohr-köre..........48
2.245 A főirányok hajlásszögének becslése..........52
2.3 A feszültségállapot vizsgálata gerendák esetében..........53
2.31 Feszültségállapot a gerendák egyes pontjaiban .............53
2.32 Főfeszültségi trajektóriák ................................58
2.4 A feszültségmező .........................59
2.41 A feszültségállapot mint a hely függvénye ..........59
2.42 Egyensúlyi egyenletek ......................................60
2.43 Statikai kerületi feltételek..................................65
3. A SZILÁRD TEST GEOMETRIAI VIZSGÁLATA..........68
3.1 Az alakváltozási állapot általános tárgyalása ................68
3.11 Feltevések, alapfogalmak....................................68
3.12 A deformációvektor, az alakváltozás-mátrix és az alakváltozás-tenzor ....................69
3.2 Az alakváltozási állapot tenzorjellegéből származó tulajdonságok ..............72
3.21 A főtengely-tétel. Speciális alakváltozási állapotok 72
3.22 Az alakváltozási tenzor Invariánsai. Fajlagos térfogatváltozás .............73
3.23 Síkbeli alakváltozási állapot ..............................75
3.24 Alakváltozási Mohr-körök..................76
3.3 Az alakváltozásmező................................................76
3.4 Geometriai egyenletek, geometriai kerületi feltételek .. 76
3.5 Összeférhetőségi (kompatibilitási) egyenletek................79
4. A LINEÁRISAN RUGALMAS TEST ANYAGEGYENLETEI ... 81
4.1 Bevezetés ..............................................................81
4.2 Az általánosított Hooke-törvény izotróp anyag esetén ... 82
4.3 Az izotróp anyag rugalmassági állandói közötti összefüggés 84
4.31 Az összefüggés levezetése..................................84
4.32 Az anyagállandók közötti összefüggés értelmezése..........87
4.4 Az általánosított Hooke-törvény alkalmazásai................88
4.41 Speciális feszültségi és alakváltozási állapotok. ... 88
4.42 Példák a feszültségállapot és az alakváltozási állapot
közötti összefüggésre .................................90
4.5 Rugalmas és nem-rugalmas alakváltozások együttese .........92
5. A RUGALMASSÁGTAN ALAPEGYENLETEI ÉS NÉHÁNY ALKALMAZÁSUK....................94
5.1 Térbeli feladatok ..................................94
5.11 A rugalmasságtan alapegyenletei..........................94
5.12 A rugalmasságtan elmozdulásmódszere..................97
5.2 Síkbeli feladatok ........................................................99
5.21 Síkbeli alakváltozási állapotú test ........................99
5.22 Síkbeli feszültségi állapota test ..........................100
5.221 Általános megjegyzések ..............................100
5.222 A tárcsaegyenlet..........................................101
5.223 A tárcsaegyenlet alkalmazásai......................105
5.224 A Saint-Venant-féle elv................................113
MUNKA-ÉS ENERGIATÉTELEK ......................................116
6.1 Általános megjegyzések................................................116
6.2 Alapfogalmak ............................................................116
6.21 A munka fogalmának általánosítása ........................116
6.22 A kiegészítő munka és általánosítása........................124
6.23 Virtuális munka..................................................127
6.24 Virtuális kiegészítő munka....................................128
6.3 Egyensúlyi feltételek ..............................129
6.31 A virtuális elmozdulások tétele ............................129
6.32 A potenciális energia állandóértékűségének tétele.......130
6.321 A potenciális energia...................131
6.322 A tétel levezetése ......................................133
6.323 Példák a potenciális energia minimum-tételének alkalmazására.......................138
6.4 Kompatibilitási feltételek ............................................142
6.41 A virtuális erők tétele..........................................142
6.411 A tétel levezetése szilárd testek esetén......142
6.42 A kiegészítő potenciális energia minimumának tétele 145
6.421 A kiegészítő potenciális energia....................145
6.422 A tétel Ismertetése........................146
6.423 Példa a (kiegészítő) alakváltozási energia minimum-tételének alkalmazására..................149
6.5 A mechanikai energia megmaradásának feltétele a rugalmasságtanban. A saját munkák tétele........151
6.51 A tétel Ismertetése..............................................151
6.52 A saját munkák tételének és a potenciális energia minimum-tételének összehasonlítása......................154
6.6 A munka- és az energiatételek áttekintése......................155
7. STABILITÁSI KÉRDÉSEK ............................................158
7.1 Bevezetés .......................................158
7.2 Az egyensúlyi állapot vizsgálata................................159
7.21 Kinetikai módszer ..........................................159
7.22 Bnergia-módszer ..........................................159
7.23 Statikai (egyensúlyi) módszer. A kritikus teher fogalma ......................162
7.24 Az első-, másod- és harmadrendű elmélet lényege........163
7.25 Példa a vizsgálati módszerek alkalmazására .... 164
7.3 A nyomott rudak kihajlása........................................169
7.31 A feladat megfogalmazása..................................169
7.32 Rugalmas kihajlás ..........................................170
7.33 Képlékeny kihajlás............................................175
7.34 A kritikus feszültség mint a karcsúsági tényező függvénye.....................175
7.35 Különböző kerületi feltételek. A kihajlási hullámhossz .................176
7.36 Alkalmazások ................................................177
7.361 Ellenőrzés ............................................178
7.362 Méretezés ............................................179
7.4 A gerendák másodrendű elmélete ............................181
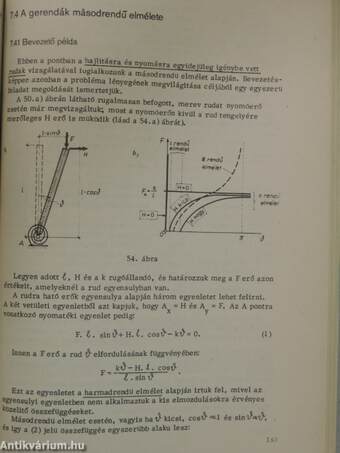
7.41 Bevezető példa................................................181
7.42 A rugalmas gerenda differenciálegyenlete a másodrendű elmélet alapján ......................................183
7.43 Példa a gerenda másodrendű elmélet szerinti differenciálegyenletének alkalmazására ................186
7.5 Egyéb stabilitási kérdések ......................................191
8. A KÉPLÉKENYSÉGTAN NÉHÁNY ALKALMAZÁSA............192
8.1 A képlékenységtan feladata ......................................192
8.2 Rúdszerkezetek képlékenységtani vizsgálata................192
8.21 Bevezető példa................................................192
8.22 Hajlított tartók teherbírásának meghatározása ...199
8.221 A képlékeny teherbírás............................199
8.222 A statikailag határozott tartók képlékeny teherbírási tartaléka................................200
8.223 A statikailag határozatlan tartók teherbírásának meghatározása ................................201
8.224 Példák statikailag határozatlan tartók teherbírásának számítására ............................207
8.3 Képlékenységi (törési) feltételek ................211
8.31 A képlékenység! (törési) feltétel fogalma...... . 211
8.32 Néhány képlékenységi (törési) feltétel .........212
8.321 Általános megjegyzések...............212
8.322 A legnagyobb normálfeszültség elmélete (Galilei-féle elmélet) ..............................213
8.323 A legnagyobb nyírófeszültség elmélete (Trescaféle elmélet).................................215
8.324 A fajlagos torzítási energia korlátozásának elmélete (Huber-Mises-Hencky-féle elmélet)..............217
8.325 A szemcsés anyagok képlékenység! feltétele (Coulomb-féle elmélet)..............................220
Ajánlott irodalom......................................223
Témakörök
- Természettudomány > Fizika > Mechanika
- Természettudomány > Fizika > Szilárdságtan
- Természettudomány > Fizika > Tankönyvek > Felsőoktatási
- Természettudomány > Fizika > Társtudományok > Műszaki
- Műszaki > Tankönyvek, jegyzetek, szöveggyűjtemények > Felsőoktatási
- Tankönyvek, jegyzetek, szöveggyűjtemények > Műszaki > Felsőoktatási > Egyéb
- Tankönyvek, jegyzetek, szöveggyűjtemények > Természettudományok > Fizika > Felsőoktatási
Megvásárolható példányok
Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.