1.066.213
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát

VISSZA
A TETEJÉRE
JAVASLATOKÉszre-
vételek
Matematikai statisztika
Ipari alkalmazásokkal
| Kiadó: | Műszaki Könyvkiadó |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Vászon |
| Oldalszám: | 352 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 25 cm x 17 cm |
| ISBN: | 963-10-0472-4 |
| Megjegyzés: | Fekete-fehér ábrákkal illusztrált. Kihajtható melléklettel. Tankönyvi szám: 60682. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Tartalom
| Előszó | 11 |
| Bevezetés | 15 |
| A valószínűségszámítás tárgyköre | 15 |
| A valószínűségszámítás feladatai | 16 |
| A matematikai statisztika problémái és módszerei | 17 |
| Valószínűségszámítási segédeszközök | 21 |
| A valószínűség fogalmára vonatkozó fontosabb ismeretek | 21 |
| Események, elemi események | 21 |
| A valószínűség. Valószínűségek összeadása | 22 |
| Feltételes valószínűség és függetlenség | 23 |
| A valószínűségi változó | 26 |
| A valószínűségi változó és típusai | 26 |
| A valószínűségi változó eloszlása | 28 |
| A valószínűségi változó jellemzői és azok tulajdonságai | 31 |
| Valószínűségi változók sztochasztikus kapcsolata | 33 |
| Két valószínűségi változó együttes eloszlása | 33 |
| Feltételes eloszlás- és sűrűségfüggvény | 35 |
| Valószínűségi változók függetlensége | 37 |
| Bayes-tétel | 38 |
| Két valószínűségi változó sztochasztkus kapcsolatának vizsgálata. Regresszió | 40 |
| A korrelációs együttható | 43 |
| Több valószínűségi változó együttes eloszlása. Függetlenség | 44 |
| Valószínűségi változó függvényének eloszlása | 46 |
| Két valószínűségi változó összegének eloszlása | 47 |
| Két független valószínűségi változó szorzatának és hányadosának eloszlása | 49 |
| Fontosabb valószínűségeloszlások | 50 |
| Normális eloszlás | 50 |
| Két- és többváltozós normális eloszlás | 52 |
| Poisson-elosztás | 53 |
| Binomiális eloszlás | 54 |
| Exponenciális és gamma-elosztás | 56 |
| Weibull-eloszlás | 57 |
| Chí a négyzeten és chí-eloszlás | 57 |
| Student- és Cauchy-eloszlás | 58 |
| Béta-eloszlások, az F-eloszlás | 59 |
| Lognormális eloszlás | 60 |
| Egyenletes eloszlás | 60 |
| Csebisev-típusú tételek. Határértéktételek | 61 |
| Csebisev-típusú tételek | 61 |
| A nagy számok törvényei | 62 |
| Határeloszlástételek | 63 |
| A mintavétel alapjai | 65 |
| A statisztikai minta | 65 |
| A mintavétel módszerei | 65 |
| Egyszerű véletlen mintavétel | 67 |
| Két- és többfokozatú mintavétel, szekvenciális módszer | 67 |
| Rétegezett mintavétel | 68 |
| Csoportos mintavétel | 68 |
| A mintabeli vagy statisztikai jellemzők | 69 |
| A statisztikai függvény fogalma | 69 |
| A tapasztalati eloszlásfüggvény | 70 |
| A legfontosabb tapasztalati jellemzők | 70 |
| Gyakorisági és sűrűséghisztogram | 72 |
| Statisztikák egyszerűsített kiszámítása | 74 |
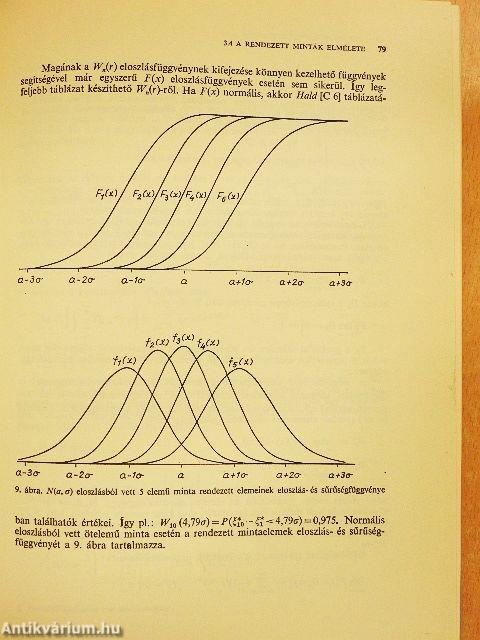
| A rendezett minták elméletének elemei | 75 |
| A rendezett mintalemek eloszlása | 75 |
| A terjedelem eloszlása | 78 |
| Glivenko tétele. A Kolmogorov-és Szmirnov-féle határeloszlástételek | 80 |
| Szmirnov, valamint Gnyegyenko és Koroljuk tételei | 81 |
| A relatív eltérés eloszlása | 82 |
| A statisztikai becslések elmélete | 83 |
| A becslési probléma | 83 |
| Torzítatlan becslések | 83 |
| A becslés hatásfoka (efficiencia) | 89 |
| Kozisztens és erősen konzisztens becslések | 92 |
| Elégséges becslések | 92 |
| A Cramér-Rao-féle egyenlőtlenség | 95 |
| Módszerek statisztikai becslések konstrukciójára | 96 |
| Intervallumbecslés. Megbízhatósági (konfidencia) intervallumok | 100 |
| Becslés rétegezett mintavétel esetén | 106 |
| Statisztikai hipotézisek vizsgálata | 110 |
| Statisztikai hipotézisek. Egyszerű és összetett hipotézis | 110 |
| Paraméteres és nemparaméteres problémák | 112 |
| A statisztikai próbák elmélete | 113 |
| A statisztikai próba | 113 |
| Az első- és másodfajú hiba valószínűsége | 113 |
| A statisztikai próbák általános tárgyalása | 118 |
| A kritikus tartomány megválasztása. Próbák összehasonlítása | 120 |
| Paraméteres próbák | 123 |
| Az u-próba | 123 |
| Az F-próba | 125 |
| A t-(Student-)próba | 127 |
| Két normális eloszlású változó várható értékének összehasonlítása ismeretlen és különböző szórások esetén | 131 |
| Több szórás megegyezésének vizsgálata, a Bartlett-próba | 133 |
| Eloszlásvizsgálat, normalitás vizsgálata, exponenciális eloszlás hipotézise | 134 |
| Események valószínűségére vonatkozó hipotézisek vizsgálata | 138 |
| Nem paraméteres próbák | |
| A chí a négyzeten-próba, alkalmazása illeszkedés-, homogenitás-, függetlenségvizsgálatra | 143 |
| A rendezett mintás próbákról általában | 153 |
| A Wilcoxon-próba | 155 |
| A Kolmogorov-Szmirnov-féle kétmintás próba | 158 |
| Előjelpróba | 160 |
| A Kolmogorov-próba | 161 |
| Szórásanalízis | 164 |
| A Fisher-Cochran-tétel | 165 |
| Egyszeres osztályozás (egyszerű csoportosítás) | 168 |
| Kétszeres osztályozás | 173 |
| A feltevésvizsgálati eljárás kölcsönhatás (interakció) nélkül | 173 |
| A teljes négyzetösszeg felbontásmódjának meghatározása a legkisebb négyzetek elve alapján | 177 |
| Eljárás kétszeres osztályozás esetén a kölcsönhatás figyelembevételével | 183 |
| Példa szórásanalízisre kétszeres osztályozás esetén | 187 |
| Háromszoros osztályozás | 191 |
| Nem teljes kísérleti elrendezések | 194 |
| A latin négyzet | 195 |
| A véletlen blokkok | 201 |
| Kiegyensúlyozott nem teljes blokkok | 204 |
| Kovarianciaanalízis | 209 |
| A probléma megfogalmazása | 209 |
| Kovarianciaanalízis egy faktor és egy kísérő változó esetén | 210 |
| Korrelázió- és regresszióanalízis | 213 |
| Bevezetés | 213 |
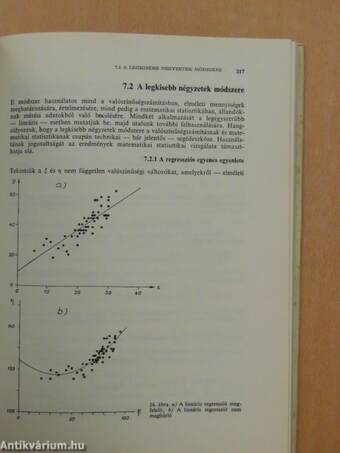
| A legkisebb négyzetek módszere | 217 |
| A regressziós egyenes egyenlete | 217 |
| A regressziós egyenes együtthatóinak becslése | 220 |
| Regressziós parabolák | 222 |
| A regressziós görbe | 224 |
| Több valószínűségi változó esete. Regressziós felület. Elméleti és tapasztalai regressziós sík | 225 |
| Ismert jellegű függvénykapcsolat ismeretlen állandóinak meghatározása. Változók közötti függvénykapcsolat közelítése | 226 |
| Megjegyzések a legkisebb négyzetek módszerének gyakorlati keresztülviteléhez | 229 |
| Korreláció- és regresszióanalízis két változó esetén | 230 |
| A korrelációs együttható becslése. A korrelációs együtthatóra vonatkozó hipotézisek vizsgálata normális eloszlás, továbbá nagy minta esetén | 230 |
| Két valószínűségi változó együttes eloszlásának statisztikai vizsgálata | 234 |
| Két változó lineáris függvénykapcsolatának statisztikai vizsgálata, ha mindkét változóban véletlen hiba lép fel | 239 |
| Normális eloszlású valószínűségi változó regressziója egy független változóra | 241 |
| Következtetés a független változóra a normális eloszlású függő változó mértékéből lineráris esetben | 245 |
| Regressziós egyenesek azonosságára, ill. párhuzamosságára vonatkozó hipotézisek normális eloszlású függő változó esetén | 247 |
| Korreláció és regresszió több változó esetén | 253 |
| Több valószínűségi változó együttes vizsgálata. Parciális és többszörös korreláció | 253 |
| Többváltozós lineáris függvénykapcsolat. A Gauss-féle normálegyenletek | 258 |
| Nemlineáris regresszió több független változó esetén | 266 |
| Elhelyezés (allokációs) problémák | 267 |
| A mérési helyek megválasztásának kérdése | 267 |
| Az alappontok megválasztása egyváltozós lineáris összefüggés regressziós együtthatójának becslésénél | 269 |
| Elhelyezés többváltozós lineáris kapcsolat esetén | 270 |
| A polinomiális regresszió alappontjainak megválasztása | 273 |
| Gyakorlati példa a regresszióanalízis felhasználására | 275 |
| A minőségellenőrzés statisztikai módszerei | 286 |
| Bevezetés | 286 |
| Gyártásellenőrzés | 287 |
| Méréses ellenőrzés | 287 |
| Minősítéses ellenőrzés | 299 |
| Az ellenőrzés időközének meghatározásáról | 304 |
| Az optimális állandó időköz meghatározása | 304 |
| Késztermék-ellenőrzés | 308 |
| A mintavételi terv | 308 |
| Egyszeres, kétszeres és többszörös mintavételi terv. A jelleggörbe | 310 |
| Az átengedett selejtátlag maximuma | 313 |
| Méréses mintavételi terv | 316 |
| Táblázatok | 319 |
| Irodalom | 342 |
| Szakkifejezések idegen nyelvű jegyzéke | 346 |
| Tárgymutató | 348 |
Témakörök
- Természettudomány > Matematika > Statisztika
- Természettudomány > Matematika > Tankönyvek > Felsőfokú
- Természettudomány > Matematika > Társtudományok > Egyéb
- Műszaki > Tankönyvek, jegyzetek, szöveggyűjtemények > Felsőoktatási
- Tankönyvek, jegyzetek, szöveggyűjtemények > Műszaki > Felsőoktatási > Egyéb
- Tankönyvek, jegyzetek, szöveggyűjtemények > Természettudományok > Matematika > Felsőfokú