1.067.053
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát

VISSZA
A TETEJÉRE
JAVASLATOKÉszre-
vételek
Matematika I.
Nyitott rendszerű képzés - távoktatás - oktatási segédlete/Tankönyv/Gábor Dénes Műszaki Informatikai Főiskola részére
| Kiadó: | LSI Oktatóközpont |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Ragasztott papírkötés |
| Oldalszám: | 407 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 24 cm x 17 cm |
| ISBN: | 963-577-131-2 |
| Megjegyzés: | Fekete-fehér ábrákkal. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Előszó
A könyv amit az Olvasó kezében tart a Gábor Dénes Műszaki Informatikai Főiskola Matematika I. tantárgyának tematikáján alapul; a matematikából azokat a területeket tartalmazza, amelyekről egy... TovábbElőszó
A könyv amit az Olvasó kezében tart a Gábor Dénes Műszaki Informatikai Főiskola Matematika I. tantárgyának tematikáján alapul; a matematikából azokat a területeket tartalmazza, amelyekről egy műszaki informatikus mérnöknek legalább áttekintéssel kell rendelkeznie.A könyv három részből áll. Az I. Részben aminek "Bevezetés a matematikába" címet adtuk a matematika több ágából kap az olvasó bevezető ismereteket (szinte összefoglaló jelleggel) a klasszikus fogalmakról, modellekről (halmaz, ítélet, komplex szám, gráf, vektor, kombinatorika). Ebben a részben nem "definíció-tétel-bizonyítás" tagolásban tárgyaljuk az anyagot (reméljük, hogy ez a megértést nem zavarja.) Vissza
Tartalom
| Bevezetés a matematikába | |
| Halmazok | 10 |
| A halmaz és megadása | 10 |
| Halmaz és részhalmaza | 12 |
| Műveletek halmazokkal | 12 |
| Rendezett n-esek | 14 |
| Halmazok direkt szorzata | 16 |
| Relációk | 15 |
| Függvények | 17 |
| Halmazok számossága | 18 |
| Végtelen számhalmazok | 19 |
| Komplex számok | 23 |
| A komplex szám fogalma | 23 |
| A komplex szám trigonometrikus alakja | 26 |
| A komplex szám exponenciális alakja | 28 |
| Miről szólt ez a fejezet? | 30 |
| Feladatok | 31 |
| Megoldások | 31 |
| Matematikai logika | 33 |
| Itéletek | 33 |
| Logikai alapműveletek | 34 |
| Logikai kifejezések | 37 |
| A matematikai logika alkalmazása a számítástechnikában | 38 |
| Miről szólt ez a fejezet? | 39 |
| Feladatok | 40 |
| Megoldások | 40 |
| Kombinatorika | 41 |
| Permutációk | 42 |
| Variációk | 45 |
| Kombinációk | 46 |
| A binomiális tétel és a Pascal-háromszög | 48 |
| Miről szólt ez a fejezet? | 49 |
| Feladatok | 50 |
| Megoldások | 50 |
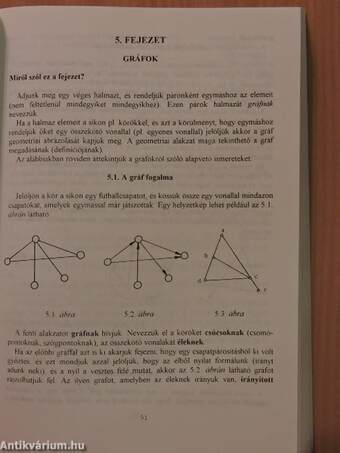
| Gráfok | 51 |
| A gráf fogalma | 51 |
| A gráfok jellemzői | 52 |
| Fák | 54 |
| A csúcsmátrix | 55 |
| A gráfok alkalmazásai | 55 |
| Miről szólt ez a fejezet? | 56 |
| Feladatok | 56 |
| Megoldások | 56 |
| Vektoralgebra | 57 |
| A vektor értelmezése | 57 |
| Műveletek vektorokkal | 58 |
| Vektorok lineáris függetlensége | 61 |
| Vektor megadása koordinátákkal | 62 |
| Vektorműveletek koordinátás megadás esetén | 63 |
| A bázisvektorok megválasztása | 68 |
| Geometriai alakzatok megadása vektorokkal | 69 |
| Néhány geometriai feladat | 73 |
| Miről szól ez a fejezet? | 81 |
| Feladatok | 87 |
| Megoldások | 88 |
| ANALÍZIS | |
| Bevezetés | 91 |
| Miről szól ez a fejezet? | 95 |
| Feladatok | 96 |
| Megoldások | 96 |
| Valós fügvények | |
| A függvény fogalma | 97 |
| Valós függvények | 98 |
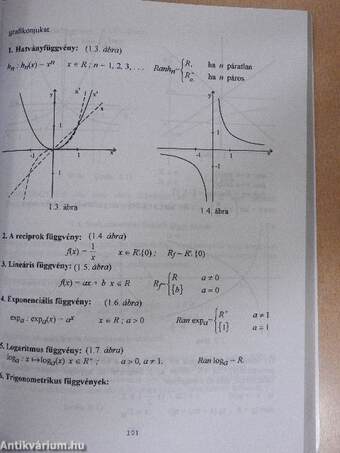
| Néhány ismert elemi függvény | 100 |
| Szakaszonként lineáris függvények | 103 |
| Műveletek valós függvényekkel | 105 |
| Korlátosság, szélősérték, monotonitás | |
| Páros és páratlan függvények | 106 |
| Polárkoordináták | 108 |
| Paraméteres egyenletek Vektor-skalár függvény | 112 |
| Miről szól ez a fejezet? | 114 |
| Számsorozatok | 115 |
| A sorozat fogalma és megadási módjai | 116 |
| Sorozatok konvergenicája, a határérték | 118 |
| Műveletek konvergens sorozatokkal | 123 |
| Monoton sorozatok | 128 |
| Nevezetes sorozatok | 132 |
| Miről szól ez a fejezet? | 132 |
| Feladatok | 133 |
| Megoldások | 134 |
| Függvények határértéke, folytonossága | 135 |
| Határérték a végesben | 135 |
| Határérték a végtelenben | 141 |
| Függvény folytonossága | 144 |
| Korlátos zárt halmazon folytonos függvények tulajdonságai | 146 |
| Az érintő | 147 |
| Miről szól ez a fejezet? | 149 |
| Feladatok | 150 |
| Megoldások | 150 |
| Elemi függvények | 151 |
| Racionális egész függvény | 151 |
| Racionális törtfüggvények | 156 |
| Inverz függvény irracionális függvények | 161 |
| Hiperbolikusz függvények és inverziek | 166 |
| Inverz trigonometrikus függvények | 171 |
| Miről szól ez a fejezet? | 173 |
| Differenciálszámítás? | 176 |
| A derviált | 177 |
| Differenciálható függvények | 179 |
| Néhány elemi függvény deriváltja | 180 |
| Differenciálási szabályok | 183 |
| A tg, ctg és a hiperbolikusz függvények deriváltja | 183 |
| Összetett függvény és függvény inverzések deriváltja | |
| Implicit függvények | 187 |
| Az exponenciális, logaritmus, arkusz és area függvények deriválása | 190 |
| A differenciál | 193 |
| Magasabbrendű deriváltak | 194 |
| A differenciálszámítás középértéktételei | 195 |
| Miről szól ez a fejezet? | 197 |
| Feladatok | 197 |
| Megoldások | 198 |
| A differenciálszámítás néhány alkalmazása | 199 |
| Görbék érintkezése, simulókör | 199 |
| Maclaurin-. és Taylor-polonom | 203 |
| A L'Hospital-szabály | 208 |
| Miről szól ez a fejezet? | 212 |
| Feladaok | 214 |
| Megoldások | 214 |
| Függvények diszkussziója a deriváltak segítségével | 215 |
| Monoton függvények | 215 |
| A szélsőérték meghatározása | 217 |
| Konvexség, konkávság, inflexiós pont | 221 |
| Miről szól ez a fejezet? | 225 |
| Feladatok | 226 |
| Megoldások | 227 |
| Határozatlan integrál | 227 |
| Primitív függvény Határozatlan integrál | 227 |
| Alapintegrálok | 229 |
| Integrálási szabályok | 229 |
| Parciális integrálás | 232 |
| Integrálás helyettesítéssel | 234 |
| Racionális törtfüggvények integrálása | 241 |
| Miről szól ez a fejezet? | 241 |
| Feladatok | 243 |
| Megoldások | 245 |
| Határozott integrál | 247 |
| A határozott integrál fogalma | 248 |
| A határozott integrál tulajdonságai | 252 |
| A Newton-Leibniz-formula | 254 |
| Folytonos függvények határozott integrálja | 257 |
| Improprius integrálok | 259 |
| Miről szól ez a fejezet? | 262 |
| Feladatok | 264 |
| Megoldások | 264 |
| A határozott integrál néhány alkalmazása | 266 |
| Területszámítás | 266 |
| A szektor területe | 270 |
| Ívhosszúság kiszámítása | 274 |
| Forgástest térfogata és felszíne | 278 |
| Miről szól ez a fejezet? | 283 |
| Feladatok | 285 |
| Megoldások | 285 |
| Többváltozós függvények | 287 |
| A kétváltozós függvény értelmezése | 287 |
| A kétváltozós függvény ábrázolása | 289 |
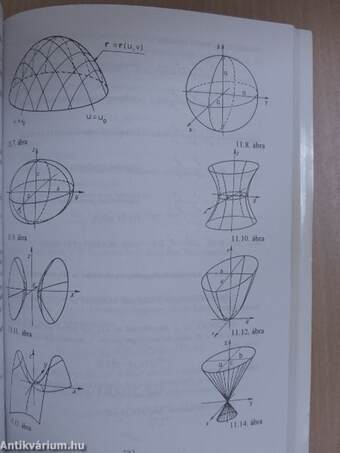
| Felületek egyenletének felírása, nevezetes felületek | 292 |
| A kétváltós függvény határértéke és folytonossága | 294 |
| A parciális derivált | 295 |
| Az iránymenti derivált | 298 |
| A teljes differenciál | 299 |
| A többváltozós függvény | 300 |
| Felület értinősíkja | 301 |
| Kétváltozós függvény szélsőértéke | 302 |
| Feltételes szélsőérték | 307 |
| Miről szól ez a fejezet? | 310 |
| Feladatok | 312 |
| Megoldások | 314 |
| Differenciálegyenletek | 317 |
| A differenciálegyenlet fogalma és osztályozása | 317 |
| A differenciálegyenlet megoldásai | 318 |
| Elsőrendű differenciálegyenletek | 320 |
| Megoldhatóság | 320 |
| Szétválasztható változójú differenciálegyenlet | 321 |
| Változókban homogén differenciálegyenlet | 324 |
| Az elsőrendű lineáris differenciálegyenlet | 325 |
| Másodrendű differenciálegyenletek | 331 |
| Hiányos másodrendű differenciálegyenlet | 331 |
| Másodrendű lineáris differenciálegyenlet | 334 |
| Magasabbrendű állandó együtthatós differenciálegyenletek | 343 |
| Miről szól ez a fejezet? | 345 |
| Feladatok | 348 |
| Megoldások | 349 |
| LINEÁRIS ALGEBRA | |
| N-dimenziós vektorok | 350 |
| A vektor fogalma | 350 |
| Speciális vektorok | 351 |
| Műveletek vektorokkal | 352 |
| Vektorok lineáris kombinációja | 354 |
| Vektorok lineáris függetlensége | 355 |
| Miről szól ez a fejezet? | 358 |
| Feladatok | 359 |
| Megoldások | 359 |
| Mátrixok | 360 |
| A mátrix értelmezése | 360 |
| Műveletek mátrixokkal | 363 |
| Elemi transzformációk | 367 |
| Mátrix determinánsa | 370 |
| A mátrix rangja | 376 |
| Négyzetes mátrix inverze | 378 |
| Miről szól ez a fejezet? | 383 |
| Feladatok | 386 |
| Megoldások | 387 |
| Lineáris egyenletrendszerek | 389 |
| A lineáris egyenletrendszer fogalma | 389 |
| A lineáris egyenletrendszer megoldhatósága | 391 |
| A Cramer-szabály | 392 |
| A Gauss-féle módszer | 394 |
| Az egyenletrendszer megoldása elemi transzformációk alkalmazásával | 398 |
| Homogén lineáris egyenletrendszerek | 401 |
| Miről szól ez a fejezet? | 404 |
| Feladatok | 406 |
| Megoldások | 407 |