1.116.650
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát
Matematika I/1.
I. éves nappali, esti és levelező tagozatos villamosmérnök-hallgatók részére/Kézirat/Budapesti Műszaki Egyetem Villamosmérnöki Kar
| Kiadó: | Tankönyvkiadó Vállalat |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Ragasztott papírkötés |
| Oldalszám: | 382 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 24 cm x 17 cm |
| ISBN: | |
| Megjegyzés: | Kézirat. 13. változatlan utánnyomás. Tankönyvi száma: J 5-357. Megjelent 354 példányban. 135 fekete-fehér ábrát tartalmaz. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Előszó
Bevezetés
A reformtanterv szellemében irt uj matematika-jegyzet a régebbinél lényegesen nagyobb anyagot uj csoportosításban foglal magában. Hogy ez a megnövekedett anyag az első tanuláskor se... Tovább
Előszó
Bevezetés
A reformtanterv szellemében irt uj matematika-jegyzet a régebbinél lényegesen nagyobb anyagot uj csoportosításban foglal magában. Hogy ez a megnövekedett anyag az első tanuláskor se tűnjék senki számára áttekinthetetlen anyaghalmaznak, gépelés-technikával igyekeztünk kiemelni azokat az anyagrészeket, melyek alapvetően fontosak a továbbhaladás, az alkalmazások szempontjából. Az anyagban elmélyülni akarók számára tett megjegyzéseket, az első tanuláskor elhagyható bizonyításokat, nagyobb margóval gépeltük és baloldalt szaggatott vonással jelöltük meg. Ezen utóbbi részek kihagyása esetén is teljes egészet alkot a jegyzet.
Külön aláhúzással szerepelnek a jegyzetben azok a definíciók, amelyekkel az alapvető fogalmakat meghatározzuk, ezeket értelemszerűen mindenkinek tudnia kell. Ugyanez áll az aláhúzással kiemelt állításokra, és a fontosabb állításokat kimondó tételekre is.
A jegyzet anyagát a matematikában tanultaknak az alaptárgyak és alapozó szaktárgyakban való jobb felhasználása érdekében a régebbi jegyzethez képest átcsoportosítottuk. A fenti szempontnak sokszor alávetettünk didaktikai szempontokat, az ebből eredő nehézségeken is a leglényegesebb anyagrészek kiemelésével, kihangsúlyozásával igyekeztünk segiteni.
Azokat a fontosabb tételeket, melyekre későbbi tárgyalásainkban is többször hivatkozunk, bizonyitjuk is, de minden kimondott tétel bizonyítására - a jegyzet korlátozott terjedelme miatt - nem törekedhettünk.
A jegyzetben tárgyalt több tétellel kapcsolatban felmerülhet az a kérdés, hogy a tételben kimondott állitás megforditható-e? Hogy egy, a középiskolából ismert állításra hivatkozunk:
Tétel; minden négyzetben a szembenfekvő oldalak egyenlők egymással. Ezen állítás nyilván nem fordítható meg, az olyan négyszögek, melyekben két-két szembenfekvő oldal megegyezik egymással, nem mind négyzetek (tetszőleges paralelogrammák is lehetnek).
Azt a tényt, hogy a fenti tételben kimondott állitás nem fordítható meg, ugy is kifejezhetjük, hogy a tételben kimondott feltétel teljesülése szükséges, de nem elégséges ahhoz, hogy egy négyszög négyzet legyen.
Vissza
Tartalom
TARTALOMJEGYZÉK
Bevezetés 3
1.) Valós számok 5
2.) A valós számok rendezése. Egyenlőtlenségek 7
3.) Abszolút érték 16
4.) Számegyenes 22
5.) Számrendszerek 25
6.) Sik- és térbeli koordinátarendszerek. Pont jellemzése a síkban és a térben 27
7.) Vektorok, müveletek vektorokkal 34
8.) Vektor felbontása összetevőkre. Vektor megadása koordinátái segítségével 44
9.) Müveletek koordinátákkal megadott vektorokkal. Alkalmazások 47
10.) Determinánsok 72
11.) A mátrix fogalma; a mátrixok fontosabb tipusai 88
12.) Mátrixok összeadása, kivonása, szorzása 93
13.) Kvadratikus mátrix determinánsa és reciproka 99
14.) A mátrix rangja. Mátrix1 diadikus felbontása 108
15.) Lineáris egyenletrendszerek megoldása. Vektorok lineáris függőségének vizsgálata 117
16.) Lineáris transzformáció 134
17.) Mátrix sajátértékei és sajátvektorai 142
18.) A halmazelmélet alapfogalmai 149
19.) Ponthalmazok. Környezet 157
20.) Számhalmazokra vonatkozó alapvető tételek 164
21.) Számsorozatok 170
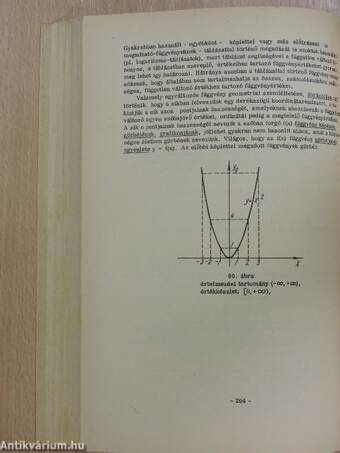
22.) A függvény fogalma és ábrázolása 201
23.) Racionális függvények 212
24.) Trigonometrikus függvények 223
25.) Periodikus függvény; páros függvény; páratlan függvény;
monoton függvény; összetett függvény; inverz függvény 235
26.) Függvény határértéke 242
27.) Folytonos függvény 255
28.) Differenciálhányados 268
29.) Differenciálási szabályok 275
30.) A differenciál fogalma 288
31.) Taylor-formula. Binomiális tétel 292
32.) A differenciálszámítás középértéktételei 300
33.) Függvényvizsgálat 304
34.) A l'Hospital-szabály 325
35.) A trigonometrikus függvények inverz függvényei. (Ciklometrikus függvények) 330
36.) Az exponenciális függvény és a logaritmus 336
37.) Hiperbolikus függvények és inverzeik 354
38.) A differenciálási szabályok rövid összefoglalása 363
39.) A differenciálhányados néhány geometriai alkalmazása. Grafikus differenciálás 365
40.) Egyenletek közelítő megoldása 371-382
Témakörök
- Természettudomány > Matematika > Algebra és számelmélet > Általában
- Természettudomány > Matematika > Analízis > Általában
- Természettudomány > Matematika > Tankönyvek > Felsőfokú
- Természettudomány > Matematika > Társtudományok > Műszaki
- Műszaki > Tankönyvek, jegyzetek, szöveggyűjtemények > Felsőoktatási
- Tankönyvek, jegyzetek, szöveggyűjtemények > Műszaki > Felsőoktatási > Egyéb
- Tankönyvek, jegyzetek, szöveggyűjtemények > Természettudományok > Matematika > Felsőfokú
Dr. Császár Ákosné
Dr. Császár Ákosné műveinek az Antikvarium.hu-n kapható vagy előjegyezhető listáját itt tekintheti meg: Dr. Császár Ákosné könyvek, művekMegvásárolható példányok
Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.