1.118.174
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát
Matematika - Biometria I.
Kézirat/Kertészeti Egyetem Matematika-Fizika Tanszék
| Kiadó: | Kertészeti Egyetem Matematika-Fizika Tanszék |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Tűzött kötés |
| Oldalszám: | 174 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 23 cm x 16 cm |
| ISBN: | |
| Megjegyzés: | Kézirat. 520 példányban jelent meg. Fekete-fehér ábrákkal illusztrálva. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Előszó
A természettudományok és a technika rohamos fejlődése lehetővé teszi, de egyúttal meg is követeli, hogy a kertészeti termesztés mind nagyobb mértékben vegye igénybe a tudományok legújabb... TovábbElőszó
A természettudományok és a technika rohamos fejlődése lehetővé teszi, de egyúttal meg is követeli, hogy a kertészeti termesztés mind nagyobb mértékben vegye igénybe a tudományok legújabb eredményeit. A modern technikai berendezések alkalmazásához, a munkaerő ésszerű felhasználásához, a munkafolyamatok korszerű megszervezéséhez az üzemet irányító kertészmérnöknek ismernie kell mindazokat a matematikai alapfogalmakat és összefüggéseket, amelyekre a gyakorlatban elvégzendő üzemszervezési és tervezési feladatok épülnek.A termesztési módszereket továbbfejlesztő szakembereknek és kutatóknak pedig szükségük van azoknak a biometriai módszereknek ismeretére, amelyek segítségével feldolgozhatják az új termesztési eljárások kipróbálását célzó kísérletek adatait.
A Kertészeti Egyetem Termesztési Szak matematika-biometria tananyaga a középiskolában tanított matematika tantárgyra épülve azokat az alapfogalmakat és műveleteket tartalmazza, amelyekkel rendelkezniök kell mind az üzemekben, mind a kutatóintézetekben dolgozó kertészmérnököknek. E jegyzet az előadások anyagának megértéséhez kíván segítséget adni a meghatározások, levezetések, mintapéldák és gyakorló feladatok összefoglalásával. Vissza
Tartalom
1. Függvénytani alapfogalmak 41.1. Függvény fogalma, megadásának módjai. Legegyszerűbb függvénytípusok. Monotonitás, periodicitás 4
1.2. Az inverz függvény fogalma. Inverz függvénypárok 10
1.3. Függvények transzformációja. Az összetett függvény fogalma 15
1.4. Feladatok 18
2. Függvények határértéke 19
2.1. Függvények határértékének definíciója végtelenben és véges helyen 19
2.2. Függvények folytonossága 31
2.3. Határértékekre vonatkozó tételek 34
2.4. Néhány fontos határérték-feladat 36
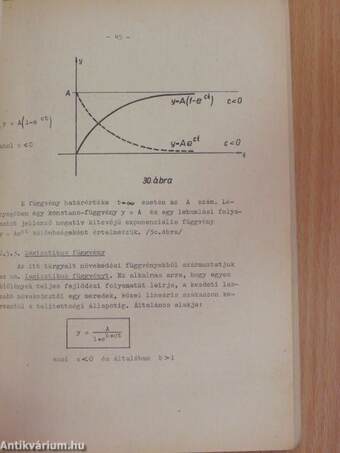
2.5. Határérték feladatok alkalmazása természeti törvényekben 42
2.6. Feladatok 47
3. A differenciálszámítás alapfogalmai 49
3.1. Függvények differenciálhányadosa. A derivált függvény 49
3.2. Általános deriválási szabályok 53
3.3. A leggyakrabban előforduló függvények derivált függvényei 58
3.4. Összefoglaló táblázat 65
3.5. Feladatok 66
4. A differenciálszámítás alkalmazása 67
4.1. A függvények menetének vizsgálata 67
4.2. Gyakorlati szélsőérték - feladatok megoldása 73
4.3. Görbék konvex és konkáv szakaszai. Inflexiós pont 76
4.4. A függvényvizsgálat általános menete 79
4.5. A differenciál 83
4.6. Feladatok 88
5. Az integrálszámítás alapfogalmai 91
5.1. A határozatlan integrál fogalma 91
5.2. Alapintegrálok 93
5.3. Integrálás helyettesítéssel 95
5.4. Parciális integrálás 97
5.5. A határozott integrál fogalma 100
5.6. Improprius integrálok 109
5.7. Feladatok 117
6. Az integrálszámítás alkalmazásai 120
6.1. Két görbe által közbezárt terület kiszámítása 120
6.2. Térfogatszámítás integrállal. Forgástest térfogata 123
6.3. Felszínszámítás integrállal. Forgástest palástjának felszíne 227
6.4. Feladatok 130
7. Integrálok közelítő értékének meghatározása 133
7.1. Téglalapszabály 133
7.2. Trapézszabály 135
7.3. A Simpson-formula 136
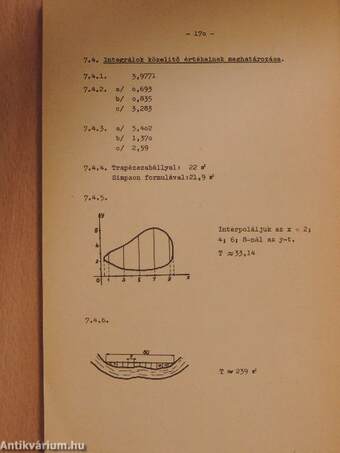
7.4. Feladatok 139
8. A többváltozós függvény alapfogalmai 141
8.1. A kétváltozós függvény fogalma, megadásának módjai, értelmezési tartománya 141
8.2. A parciális differenciálhányados 147
8.3. A teljes differenciál 148
8.4. A teljes differenciál alkalmazása hibaszámításnál 148
8.5. Feladatok 149
Feladatok megoldása 151
1.4. Függvénytani alapfogalmak 151
2.6. Függvények határértéke végtelenben és véges helyen 159
3.5. Differenciálszámítás 162
4.6. A differenciálszámítás alkalmazása 164
5.6. Integrálszámítás 167
6.4. Az integrálszámítás alkalmazásai 169
7.4. Integrálok közelítő értékeinek meghatározása 170
8.5. Többváltozós függvények 171
Megvásárolható példányok
Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.