1.118.362
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát
Matematika
Középiskolai tanulók, főiskolai- és egyetemi hallgatók valamint műszaki- és gazdasági szakemberek számára, gyakorlati alkalmazásokkal
| Kiadó: | Scolar Kiadó |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Fűzött kemény papírkötés |
| Oldalszám: | 813 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 17 cm x 12 cm |
| ISBN: | 963-853-414-1 |
| Megjegyzés: | Fekete-fehér ábrákkal illusztrálva. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Tartalom
| Részlet az első kiadás előszavából | 5 |
| Részlet a harmadik kiadás előszavából | 5 |
| Előszó a tizenharmadik kiadáshoz | 5 |
| Általános matematikai jelölések | 13 |
| A halmazelmélet és az absztrakt algebra elemei | 19 |
| Halmazok | 19 |
| Műveletek halmazokkal | 23 |
| A matematikai logika néhány fogalmának és jelölésének használatáról | 29 |
| Az absztrakt algebra elemei | 30 |
| A csoport fogalma, csoportaxiómák | 31 |
| A test fogalma, testaxiómák | 32 |
| Számtan (Aritmetika) | 36 |
| Természetes egész számok | 36 |
| A valós számok halmaza | 36 |
| A valós számegyenes | 39 |
| A természetes számok halmaza | 40 |
| Műveletek természetes számok halmazában | 48 |
| A négy alapművelet sorrendje, zárójelek használata | 49 |
| Oszthatóság | 51 |
| Prímszám, összetett szám, prímtényezőkre bontás és hatványozás | 52 |
| A legnagyobb közös osztó | 54 |
| A legkisebb közös többszörös | 55 |
| A teljes indukció | 57 |
| Az egész számok halmaza | 59 |
| A számok abszolút értéke és nagysági viszonyai | 60 |
| Műveletek a Z halmazban (az egész számok halmazában) | 63 |
| Műveletek nullával | 64 |
| A racionális számok Q halmaza | 67 |
| Törtszámok egyszerűsítése és bővítése | 68 |
| Törtszámok összehasonlítása, közös nevezőre hozásuk | 69 |
| Műveletek a racionális számok halmazában | 73 |
| Műveletek tizedes törtekkel | 74 |
| Közönséges és tizedes törtek kapcsolata | 76 |
| Százalékszámítás | 78 |
| A közelítő számítás, és a kerekítés néhány szabálya | 78 |
| Arány és aránypár | 81 |
| Az irracinálás és a valós számok halmaza (Q*, R) | 84 |
| Axiómák | 85 |
| Intervallum, távolság, környezet | 87 |
| A megszámlálható és a nem megszámlálható halmazok | 91 |
| Számtani, mértani, harmonikus és négyzetes középarányos | 95 |
| Algebra | 98 |
| Az algebrai írásmód | 98 |
| Műveletek algebrai mennyiségekkel | 99 |
| Műveletek egytagú algebrai kifejezésekkel: többtagúak összeadása és kivonása | 102 |
| Többtagú algebrai kifejezések szorzása: nevezetes szorzatok | 106 |
| Az R halmazba tartozó számok négyzetének és köbének kiszámítása | 111 |
| Többtagú algebrai kifejezések osztása | 112 |
| Többtagú algebrai kifejezések szorzattá alakítása | 115 |
| Algebrai törtkifejezések | 117 |
| Műveletek hatványmennyiségekkel | 121 |
| Gyökvonás. Műveletek gyökmennyiségekkel. | 125 |
| Algebrai összegek és valós számok négyzetgyöke | 133 |
| A kettes (bináris) és nyolcas (oktális) számrendszer | 136 |
| Logaritmus | 139 |
| Egytagú algebrai kifejezések logaritmusa. A logaritmus azonosságai | 142 |
| Logaritmusrendszerek és összefüggéseik | 145 |
| Számolás 10-es alapú logaritmusokkal | 147 |
| Az egyenletek fogalma és osztályozása | 151 |
| Az egyenlet rendezésének szabályai | 158 |
| Szöveges egyenletek | 161 |
| Elsőfokú (lineáris) kétismeretlenes egyenletrendszer megoldása és a determináns fogalma | 165 |
| Elsőfokú (lineáris) kettőnél több ismeretlenes egyenletrendszer megoldása | 172 |
| Elsőfokú (lineáris) homogén egyenletrendszer megoldása | 183 |
| Másodfokú egyismeretlenes egyenlet megoldáa | 187 |
| Összefüggés a másodfokú egyenlet gyökei és együtthatói között | 190 |
| Másodfokú egyenlet gyöktényezős alakja | 195 |
| Magasabbfokú és négyzetgyökkifejezést tartalmazó egyenletek | 196 |
| Másodfokú kétismeretlenes egyenletrendszer megoldása | 199 |
| Exponenciális és logaritmikus egyenletek megoldása | 205 |
| Egyenlőtlenségek alaptulajdonságai | 207 |
| Első- és másodfokú egyismeretlenes egyenelőtlenségek, egyenlőtlenségrendszerek megoldása | 215 |
| A kombinatorika és a valószínűségszámítás elemei | 223 |
| Kombinatorika | 223 |
| Ismétlés nélküli és ismétléses permutációk | 223 |
| Ismétlés nélküli és ismétléses variációk | 226 |
| Ismétlés nélküli és ismétléses kombinációk | 230 |
| A binomiális tétel és a binomiális együtthatók tulajdonságai | 234 |
| A valószínűségszámítás elemei | 240 |
| Az eseményalgebra alapfogalmai | 241 |
| A valószínűség tapasztalati megközelítése | 244 |
| A valószínűség matematikai fogalma | 244 |
| A valószínűség klasszikus fogalma | 246 |
| Geometriai valószínűségek | 250 |
| Feltételes valószínűség és függetlenség | 251 |
| A valószínűségi változó fogalma | 255 |
| Néhány fontosabb eloszlás | 260 |
| A valószínűségi változók jellemző adatai | 262 |
| Geometria | 267 |
| Síkmértan | 267 |
| A geometria tárgya, felosztása és fejlődése | 267 |
| Pont és vonal | 269 |
| Szögek és szögpárok | 271 |
| Háromszöveg | 277 |
| Háromszögek egybevágósága | 280 |
| Négyszögek | 284 |
| Sokszögek | 291 |
| Az egy ponton átmenő egyenesre (egyenesseregre) vonatkozó tételek | 192 |
| A háromszögek hasonlósága | 194 |
| Osztókörző, léptékmérő és pantográf | 196 |
| Arányos távolságok a derékszögű háromszögen. Pitagorasz tétele | 198 |
| Kör | 300 |
| Arányos távolságok a körben | 309 |
| Körbe és kör köré írt háromszögek és négyszögek | 311 |
| A síkidomok kerülete és területe | 315 |
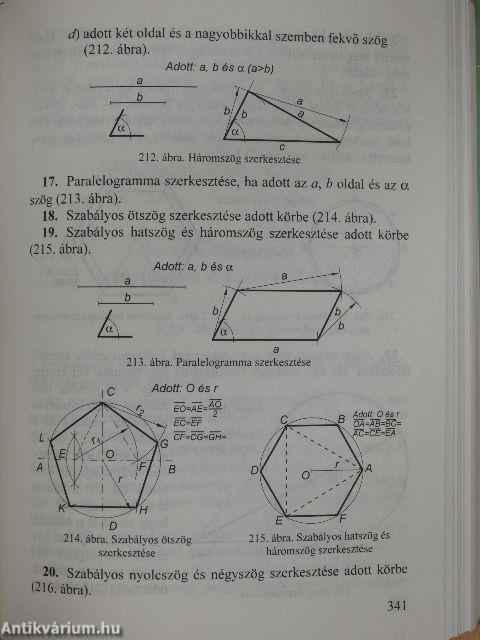
| Geometriai szerkesztések | 335 |
| Térgeometria (Térmértan, Sztereometria) | 343 |
| Alapfogalmak | 343 |
| A testek osztályozása, poliéderek, Euler tétele, szabályos testek | 347 |
| Speciális poliéderek | 350 |
| Görbefelületű testek | 357 |
| Trigonometria | 373 |
| Hegyesszögek szögfüggvényeinek értelmezése | 373 |
| Alapösszefüggések ugyanazon szög szögfüggvényei között | 375 |
| Néhány speciális szög szögfüggvényei | 379 |
| Trigonometrikus függvényértékek és logaritmusok táblázata | 381 |
| Derékszögű háromszög megoldása | 385 |
| Szögfüggvények általánosítása | 393 |
| Általános háromszög megoldása: szinusz- és koszinusztétel | 398 |
| Összegezési (addíciós) tételek | 405 |
| A kétszeres és a félszöveg függvényei | 407 |
| Két szinusz- vagy koszinuszfüggvény összegének és különbségének átalakítása szorzattá | 410 |
| Trigonometrikus egyenletek | 414 |
| A gömbi trigonometria alapfogalmai | 432 |
| Gömbháromszög szinusztétele | 435 |
| Gömbháromszög koszinusztétele | 346 |
| Két földrajzi hely távolságának meghatározása | 348 |
| Koordinátageometria (Analitikus geometria) | 440 |
| A pont derékszögű koordinátái a síkon | 440 |
| A pont koordinátáihoz kapcsolódó alapfeladatok | 442 |
| Az egyenes egyenletei | 445 |
| Az egyenessel kapcsolatos alapfeladatok | 452 |
| Koordinátatranszformáció | 461 |
| A kör és egyenletei | 463 |
| A kör érintőjének egyenlete | 465 |
| Az ellipszis és egyenletei | 467 |
| Az ellipszis érintőjének és aszimptótáinak egyenlete | 472 |
| A hiperbola és egyenletei | 474 |
| A hiperbola érintőjének és aszimptótáinak egyenlete | 480 |
| A parabola és egyenletei | 482 |
| A parabola érintőjének egyenlete | 486 |
| Síkbeli polárkoordinátarendszer | 488 |
| Görbék paraméteres egyenletei | 490 |
| Másodrendű görbék | 492 |
| A pont Descartes-féle koordinátái a térben | 496 |
| A térbeli pont koordinátáihoz kapcsolodó alapfeladatok | 498 |
| A sík egyenletei | 503 |
| A térbeli egyenes egyenletei | 507 |
| Síkkal és egyenessel kapcsolatos feladatok | 512 |
| Vektoralgebra | 520 |
| Skaláris és vektormennyiségek | 520 |
| Vektorok szorzása skaláris mennyiséggel. Egységvektor | 521 |
| Vektorok összege és különbsége | 523 |
| Vektorok derékszögű koordinátái | 525 |
| Két vektor skaláris szorzata | 527 |
| Két vektor vektoriális szorzata | 531 |
| Három vektor vegyes szorzata | 534 |
| A vektoralgebra geometriai alkalmazása | 536 |
| Példák a vektoralgebra mechanikai alkalmazására | 544 |
| Komplex számok algebrája | 548 |
| Komplex számok bevezetése | 548 |
| A komplex számtest | 549 |
| A komplex számok algebrai alakjai | 552 |
| A komplex számok ábrázolása, trigonometrikus alakja. Alapműveletek | 554 |
| Hatványozás és gyökvonás a komplex számtestekben | 560 |
| Bevezetés az analízisbe | 566 |
| Relációk | 566 |
| Függvények | 571 |
| Injekció, szuperjekció és bijekció | 574 |
| A függvények leszűkítése, kompozíciója, inverze és ábrázolása | 576 |
| Számsorozatok | 580 |
| A sorozat határértéke | 583 |
| Számtani sorozat | 587 |
| Mértani sorozat | 591 |
| A függvény határértéke | 597 |
| A függvény folytonossága | 606 |
| Elemi függvények és grafikonjaik | 609 |
| Elemi függvénytranszformációk | 629 |
| A lineáris interpoláció és az egyenletek közelítő megoldása | 634 |
| A differenciálszámítás és néhány alkalmazása | 641 |
| A differenciálhányados | 641 |
| A deriváltfüggvény | 643 |
| A differenciálás szabályai és az elemi függvények differenciálhányadosa | 645 |
| Középértéktétel. A differenciál fogalma, geometriai jelentése és alkalmazása | 657 |
| Magasabbrendű deriváltak | 662 |
| Függvényvizsgálat, szélsőérték, inflexiós pont | 664 |
| Az integrálszámítás és néhány alkalmazása | 671 |
| A határozatlan integrál | 672 |
| A határozott integrál és tulajdonságai | 677 |
| Néhány függvénytípus integrálása | 694 |
| A határozott integrál, mint határérték | 701 |
| A határozott integrál alkalmazása | 705 |
| Közönséges differencálegyenletek | 719 |
| A differenciálegyenletek fogalma és osztályozása | 719 |
| A differenciálegyenlet megoldása | 721 |
| Görbesereg differenciálegyenlete | 721 |
| Szétválasztható változójú elsőrendű differenciálegyenlet | 725 |
| Néhány szétválasztható változójúra visszavezethető elsőrendű differenciálegyenlet | 727 |
| Elsőrendű lineáris differenciálegyenlet | 729 |
| Bernoulli-féle differenciálegyenlet | 736 |
| Riccati-féle differenciálegyenlet | 738 |
| Egzakt differenciálegyenlet | 740 |
| Görbesereg burkológörbéje, és az elsőrendű differenciálegyenlet szinguláris megoldása | 742 |
| Lagrange- és Clairaut-féle differenciálegyenlet | 744 |
| Példák elsőrendű differenciálegyenletek műszaki alkalmazására | 748 |
| Hiányos másodrendű differenciálegyenletek | 751 |
| Másodrendű, állandó együtthatójú homogén lineáris differenciálegyenlet | 758 |
| Másodrendű, állandó együtthatójú inhomogén lineáris differenciálegyenlet megoldása kísérletező feltevéssel | 762 |
| Másodrendű, állandó együtthatójú inhomogén lineáris differenciálegyenlet megoldása kísérletező feltevéssel | 765 |
| Euler-féle lineáris másodrendű differenciálegyelet | 769 |
| Példák másodrendű differenciálegyenletek műszaki alkalmazására | 775 |
| Differenciálegyenlet-rendszer visszavezetése egy magasabbrendű differenciálegyenletre | 779 |
| Állandó együtthatójú lineáris differenciálegyenlet-rendszer | 784 |
| Példák differenciálegyenlet-rendszerek műszaki alkalmazására | 787 |
| Gyakran előforduló állandók | 794 |
| Irodalom | 798 |
| Név- és tárgymutató | 799 |
Témakörök
Obádovics József Gyula
Obádovics József Gyula műveinek az Antikvarium.hu-n kapható vagy előjegyezhető listáját itt tekintheti meg: Obádovics József Gyula könyvek, művekMegvásárolható példányok
Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.