1.118.551
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát
Matematika
232 színes oldal, 2351 tárgyszó
| Kiadó: | Springer Hungarica |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Fűzött kemény papírkötés |
| Oldalszám: | 484 oldal |
| Sorozatcím: | SH atlasz |
| Kötetszám: | 7 |
| Nyelv: | Magyar |
| Méret: | 21 cm x 14 cm |
| ISBN: | 963-7775-60-9 |
| Megjegyzés: | Színes ábrákkal. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Tartalom
| Jelölések és rövidítések | 7 |
| A matematika részterületei | 12 |
| Matematikai logika | |
| Kijelentések és ezek összekapcsolása | 14 |
| Kijelentések és prédikátumok logikája | 16 |
| Prédikátumok logikájának kiterjesztése | 18 |
| A bizonyítás és definiálás formái | 20 |
| Halmazelmélet | 22 |
| Alapfogalmak | 24 |
| Rendszerelmélet | 26 |
| A halmazemélet problematikája | 28 |
| Relációk és struktúrák | |
| Relációk | 30 |
| Leképezések, függvények | 32 |
| Számosság, kardinális számok, megszámlálhatóság | 36 |
| Struktúrák elmélete | 38 |
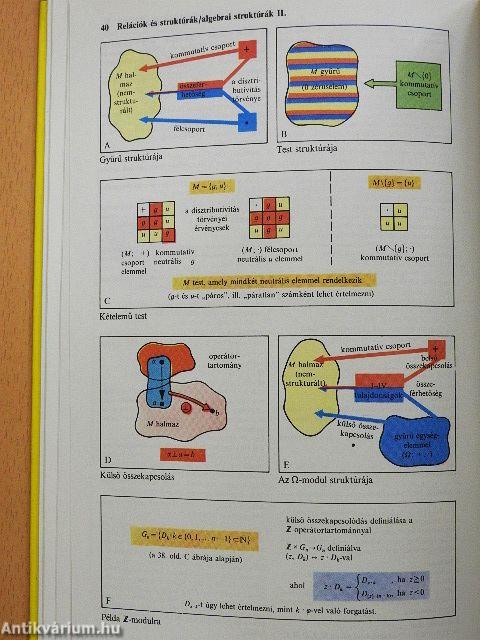
| Algebrai struktúrák I-II. | 42 |
| Rendezési struktúrák I-II. | 46 |
| Rendszámok I-II. | 46 |
| Topologikus struktúrák | 50 |
| A számrendszer felépítése | |
| A természetes számok felcsoportja | 54 |
| Az egész számok gyűrűje | 56 |
| A racionális számok teste | 56 |
| Valós számok I-III. | 58 |
| Komplex számok I-II. | 64 |
| Összefoglalás, általánosítás | 68 |
| Algebra | |
| Áttekintés | 70 |
| Csoportelmélet I-IV. | 72 |
| Gyűrűk és testek I-II. | 80 |
| Modulusok és vektorterek I-II. | 84 |
| Lineáris leképzések, mátrixok, determinánsok I-II. | 92 |
| Egyenletek, egyenletrendszerek | 92 |
| Polinomgyűrűk I-III. | 94 |
| Testek bővítése I-III. | 98 |
| Prímszámtestek, véges testek | 104 |
| GALOIS-ELMÉLET I-II. | 106 |
| A GALOIS-ELMÉLET alkalmazásai I-II/2. | 110 |
| Számelmélet | |
| Az oszthatóság elmélete integritástarományokban I-III. | 116 |
| Diophantosi egyenletek, hatványmaradékok | 120 |
| Értékeléselmélet I-III. | 122 |
| A prímszámok elmélete | 126 |
| Geometria | |
| Áttekintés | 128 |
| Geometriai alapfogalmak | 130 |
| Abszolút geometria I-II. | 132 |
| Metrijus euklideszi és nemeuklideszi geometria | 136 |
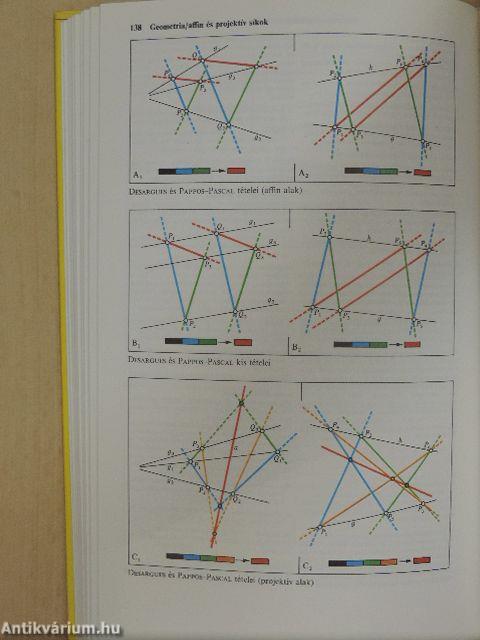
| Affin és projektív síkok | 138 |
| Kollineációk és korrelációk | 140 |
| Ideális sík, koordinátok bevezetése | 142 |
| Projektív metrika | 144 |
| Rendezés és irányítás | 148 |
| Szögek és szögmérés | 150 |
| Kongruencia-leképzések I-III. | 156 |
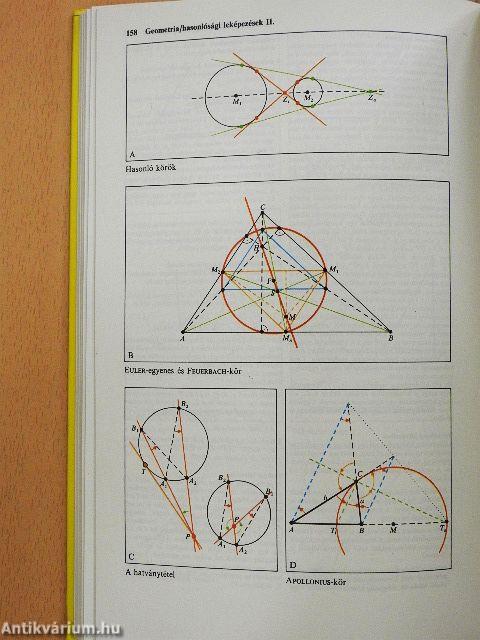
| Hasonlósági leképzések I-II. | 156 |
| Affin leképzések I-II. | 164 |
| Projektív leképezések I-II. | 168 |
| A leképezés egyenletei | 170 |
| Speciális felületek és testek I-II. | 172 |
| Ábrázoló geometeria I-II. | 174 |
| Trigonometria I-II. | 178 |
| Hiperbolikus geometria I-II. | 182 |
| Elliptikus geometria I-II. | 186 |
| Analitikus geometria | |
| A V 3 vektortér | 190 |
| Skaláris szorzat, vektoriális szorzat, vegyes szorzat | 192 |
| Egyenesek, és síkok egyenlete | 194 |
| Gömb, kúp, kúpszeletek | 196 |
| Affin leképzeések R3-ban, mozgások | 198 |
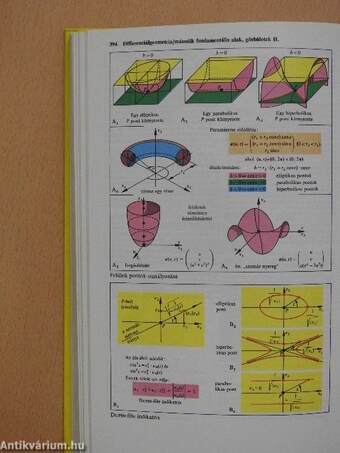
| Másodrendű felületek I-II. | 200 |
| Az R n geometriája I-II. | 204 |
| Topológia | |
| Áttekintés | 206 |
| A topologikus leképezés szemléletes értelmezése | 206 |
| Topológiai alapfogalmak szemléletes értelmezése I-II. | 210 |
| A toplogikus tér definíciója | 214 |
| Metrikus tér, bázis, albázis, környezeti bázis | 216 |
| Topologikus terek leképezése, alterek | 218 |
| Hányadostér, szorzattér, egyesített tér | 220 |
| Összefüggőség, összefüggőség utak szempontjából | 222 |
| Sorozatok és szűrőbázisok konvergenciája | 224 |
| Szétválasztási axiómák | 228 |
| Kompaktság | 230 |
| Metriziálhatóság | 232 |
| Dimenzióelmélet | 232 |
| Görbék | 234 |
| Algebrai topológia | |
| Homotópia I-II. | 236 |
| Poliéderek I-II. | 240 |
| Poliéderek fundamentális csoportja | 244 |
| Felületek | 246 |
| Homológiaelmélet | 248 |
| Gráfelmélet | |
| Gráfelmélet I-III. | 250 |
| A valós analízis alapjai | |
| Struktúrák R-en | 256 |
| Sorozatok és sorok I-III. | 258 |
| Valós függvények I-IV. | 264 |
| Differenciálszámítás | |
| Áttekintés | 272 |
| Differenciálható valós függvények I-II. | 274 |
| Középértéktételek | 278 |
| Sorbafejtések I-II. | 284 |
| Racionális függvények I-II. | 288 |
| Algebriai függvények | 290 |
| Nemalgebrai függvények I-II. | 290 |
| Közelítés | 294 |
| Interpoláció | 296 |
| Egyenletek numerikus megoldása | 298 |
| Differenciálszámítás az Rn-ben I-IV. | 300 |
| Integrálszámítás | |
| Áttekintés | 310 |
| RIEMANN-integrál | 312 |
| Integrálási szabályok, R-integrálható függvények | 314 |
| Primitív függvények, határozatlan integrál | 316 |
| Integrálási módszerek, sorok integrálása | 318 |
| Integráltáblázat I-II. | 320 |
| Közelítő eljárások, improprius integrálok | 322 |
| Többváltozós függvények, RIEMANN-integrálja | 324 |
| Többszörös integrálok, térfogatszámítás, helyettesítés | 326 |
| RIEMANN-féle összegek és alkalmazásuk I-II. | 328 |
| Görbemeneti integrálok, felületi integrálok I-II. | 332 |
| Integráltételek | 336 |
| JORDAN-mérték és LEBESGUE-mérték I-II. | 338 |
| Mérhető függvények, LEBESGUE-integrál I-II. | 342 |
| Funkciónálanalízis | |
| Absztrakt terek I-II. | 346 |
| Differenciálható operátorok | 349 |
| Variációszámítás | 350 |
| Integrálegyenletek | 352 |
| Differenciálegyenletek | |
| A differenciálegyenlet fogalma | 354 |
| Elsőrendű differenciálegyenletek I-III. | 356 |
| Másodrendű differenciálegyenletek | 362 |
| N-edrendű lineáris differenciálegyenletek | 364 |
| Differenciálegyenlet-rendszerek I-II. | 366 |
| Tételek az egzisztenciára és egyértelműségre | 370 |
| Numerikus módszerek | 372 |
| Differenciálgeometria | |
| Görbék az R3-ban I-V. | 374 |
| Síkgörbék | 284 |
| Felületdarabok, felületek I-II. | 386 |
| Első fundamentális alak | 390 |
| Második fundamentális alak, görbületek I-III. | 392 |
| Főtétel | 398 |
| Tenzorok I-II. | 400 |
| Sokaságok, RIEMANN-geometria I-II. | 402 |
| Függvénytan | |
| Áttekintés | 406 |
| Komplex számok, kompakttátétel | 408 |
| Komplex sorozatok és függvények | 410 |
| Holomorfizmus | 412 |
| CAUCHY integráltétele és integrálképletei | 414 |
| Hatványsorok | 416 |
| Analitikus folytatás | 418 |
| Szingularitások, LAURENT-sorok | 420 |
| Meromorfizmus, reziduum | 422 |
| RIEMANN-felületek I-II. | 424 |
| Egész függvények | 428 |
| Meromorf függvények C-n | 430 |
| Periodikus függvények | 432 |
| Algebrai függvények | 434 |
| Konform leképezések I-II. | 436 |
| Többváltozós függvények I-II. | 440 |
| Kombinatorika | |
| Problémák és módszerek I-II. | 444 |
| Valószínűségszámítás és statisztika | |
| Esemény és valószínűség I-II. | 448 |
| Eloszlások I-II. | 452 |
| Statisztikai módszerek I-II. | 456 |
| Lineáris optimálás | |
| A probléma felvetése | 460 |
| Szimplex módszer I-II. | 462 |
| Tárgymutató | 466 |