1.118.322
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát
Logikai rendszerek és szekvenciális automaták
Kézirat/Budapesti Műszaki Egyetem Villamosmérnöki Kar
| Kiadó: | Tankönyvkiadó Vállalat |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Ragasztott papírkötés |
| Oldalszám: | 426 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 24 cm x 17 cm |
| ISBN: | |
| Megjegyzés: | Kézirat. Tankönyvi szám: J5-1184. Megjelent 780 példányban. 261 fekete-fehér ábrával. Kihajtható mellékletekkel. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Előszó
Műszaki feladatok logikai modellekre alapozott tárgyalása nem régi keletű. A XIX. és XX. század fordulóján terjedni kezdő, vasútbiztosító berendezések és telefonközpontok tervezése során vetődött... TovábbElőszó
Műszaki feladatok logikai modellekre alapozott tárgyalása nem régi keletű. A XIX. és XX. század fordulóján terjedni kezdő, vasútbiztosító berendezések és telefonközpontok tervezése során vetődött fel először az igény olyan matematikai módszerek kidolgozására, melyek segítségével az akkor még elsősorban mechanikus, ill. elektromechanikus elven működő kapcsolókból felépülő rendszerek elméleti tárgyalása lehetővé válhatott. Az elvi alapokat valójában George Boole már a múlt század közepén kidolgozta, de hosszú időnek kellett még eltelni, míg felismerték, hogy Boole eredményei a két fizikai állapottal rendelkező kapcsolókból felépülő műszaki berendezések tárgyalásánál rendkívül jól felhasználhatók.A "Kapcsoláselmélet", "Logikai kapcsolás tan", "Switching Theory", "Theorie der Schaltnetzwerke", "Algebra dvupoljusznüh szkhem", stb. irodalmi címszavakkal megjelölt tudományág tényleges fejlődésének megindulását századunk 30-as éveitől számítjuk, mikor C.E. Shannon és W.I. Sesztakov, reléhálózatok logikai modellekkel történő tárgyalását bemutató alapvető cikkei megjelentek. A közbejött világháború haditechnikai igényei nagymértékben fellendítették a témakör fejlődését, mely a háború utáni években az absztrakt automaták elméletének kidolgozásával, az elektronikus-félvezető elemek, majd az integrált áramkörök megjelenésével még rohamosabban folytatódott és napjainkban a hírközléstechnika, irányítástechnika, számítógéptechnika és még jónéhány szakterületnek fontos alaptudományává vált.
Jelen jegyzet villamosmérnök hallgatók részére íródott és a Híradástechnika Szak "Logikai Kapcsolástan" tantárgy tantervének megfelelő anyagot öleli fel, ennek értelmében a kapcsoló elemekből (kapukból, tárolókból, stb.) felépülő kombinációs és szekvenciális logikai rendszerek szintézis és analízis módszereivel foglalkozik elsősorban. A realizációs elemek belső áramköri kérdéseit csak a szükségletnek megfelelő mélységben érinti, mivel ezek részletes tárgyalása más szaktárgyak feladatkörébe esik. Másoldalról, nem foglalkozik a jegyzet nagyobb logikai rendszerek (pl. számítógépek, automatikai berendezések, stb.) 111. ezek sajátos feladatainak (pl. regiszter-operációk, stb.) tárgyalásával, mivel ezek már ugyancsak más szaktárgyakhoz tartoznak. Vissza
Tartalom
BEVEZETÉS 31. fejezet 5
LOGIKAI MODELL 5
1.1 A logikai modell előállítása 5
1.2 Kódolási alapok 7
1.2.1 Definíciók 7
1.2.2 Néhány fontosabb kód 8
1.2.3 A Hamming-féle távolság 11
2. fejezet 12
LOGIKAI FÜGGVÉNYEKKEL KAPCSOLATOS ALAPFOGALMAK 12
2.1 A logikai függvény fogalma 12
2.2 Logikai függvények leírásmódjai 13
2.3 Egy-, két- és többváltozós logikai függvények 16
2.4 Funkcionális teljesség Bázisrendszerek 23
2.5 Funkcionális teljesség és a realizáció problémái 27
2.6 A matematikai logika néhány alapfogalmáról 27
3. fejezet
LOGIKAI FÜGGVÉNYEKET REALIZÁLÓ ÁRAMKÖRÖK
3.1 Matematikai absztrakció és áramköri megvalósítás 30
3.1.1 Néhány alapvető fogalom és konvenció 3q
3.1.2 Valóságos és ideális működés 32
3.2 Elektronikus logikai áramkörök 33
3.2.1 Klasszikus félvezetős logikai áramkörök 35
3.2.2 Integrált logikai áramkörök 43
3.3 Elektromechanikus felépítésű logikai áramkörök 54
3.3.1 Jelfogós logikai áramkörök. Jelfogók fajtái és jelölések 54
3.3.2 Jelfogós logikai kapcsolások 57
4. fejezet 60
LOGIKAI ALGEBRÁK, KANONIKUS ALAKOK 60
4.1 A NEM-ÉS-VAGY függvényekre épülő funkcionálisan teljes
rendszer 60
4.1.1 Dualitás 61
4.1.2 Boole algebrai azonosságok 62
4.2 SHEFFER és PEIRCE függvényekre épülő funkcionálisan
teljes rendszerek 64
4.2.1 Sheffer és Peirce algebrai azonosságok 64
4.2.2 Kombinált algebra 56
4.3 Logikai függvények transzformációs formulái egyéb funkcionálisan teljes rendszerekben 66
4.4 Logikai függvények kanonikus alakja 67
4.4.1 Diszjunktiv és konjunktív kanonikus alakok 57
4.4.2 Szabályos alakok teljes spektruma 72
4.4.3 Veitch-Karnaugh táblák és kanonikus alakok 78
5. fejezet
KOMBINÁCIOS HÁLÓZAT FOGALMA. OPTIMÁLIS HÁLÓZAT ELŐÁLLÍTÁSÁVAL KAPCSOLATOS MEGGONDOLÁSOK 87
5.1 Definiciők és meggondolások 87
5.1.1 Matematikai absztrakció és realizálás 37
5.1.2 Részbeni és teljes meghatározottság 90
5.2 Optimális hálózat előállításával kapcsolatos kérdések 92
5.2.1 Kombinációs hálózatok tervezésével kapcsolatos
meggondolások
5.2.2 A logikai függvény minimál alakjával kapcsolatos
alapvető definíciók és fogalmak
5.2.3 Transzformációk, dekompozíció, közös komponensek 98
6. fejezet 100
SZISZTEMATIKUS MINIMALIZÁLÁSI ÉS ÁTALAKÍTÁSI
ELJÁRÁSOK 100
6.1 Algebrai szabályok közvetlen alkalmazásának módszere 100
6.1.1 Kétszintes logikák 100
6.1.2 Többszintes logikák 102
6.2 Grafikus módszerek 105
6.2.1 Legnagyobb tömbök előállításának módszere 105
6.2.2 Gátlási elv 108
6.2.3 Többfokozatú hálózat előállítása a gátlási elv konzekvens
alkalmazásával 109
6.2.4 Közös részhálózatok kialakítása többkimenetű kombinációs hálózatnál 113
6.3 Táblázatos módszerek. QUINE-Mc. CLUSKEY módszer 117
6.3.1 Egykimenetü, teljesen meghatározott kombinációs
hálózat esete
6.3.2 Részben meghatározott (DON' T CARE) függvénnyel leírt
kombinációs hálózat esete 120
6.3.3 Közös részhálózatok kialakítása többkimenetű kombinációs
hálózatnál 128
7. fejezet 130
LOGIKAI FÜGGVÉNYEK DEKOMPOZICIÓJA 130
7.1 A dekompozíció problémaköre 130
7.1.1 Alapfogalmak 130
7.1.2 A de kompozíciók osztályozása 132
7.2 Egyszerű diszjunkt dekompozíció 132
7.2.1 Egy bevezető példa 134
7.2.2 Következtetések 136
7.2.3 Exisztencia tétel 138
7.2.4 Szisztematikus eljárás 139
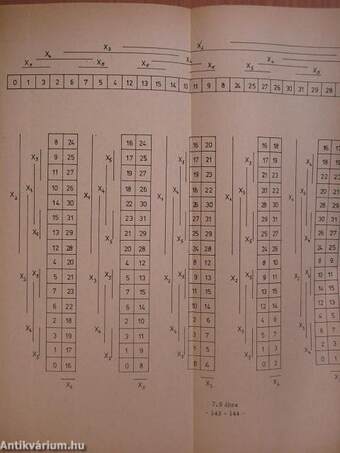
7.3 Összetett diszjunkt dekompozíció 148
7.3.1 Az összetett diszjunkt dekompozíció főbb típusai és
felépítésük 153
7.3.2 Szisztematikus módszer 154
7.4 További lehetőségek 161
7.4.1 Konjunkt dekompozíció 161
7.4.2 Dekompozició bővítéssel illetve csonkítással 161
8. fejezet 164
SZIMMETRIKUS FÜGGVÉNYEK ÉS NÉHÁNY JELLEGZETES
ÁRAMLOGIKÁS HÁLÓZATTÍPUS 164
8.1 Szimmetrikus függvények fontosabb tulajdonságai 164
8.1.1 Skalár jellemzők 164
8.1.2 Egyszerű szimmetrikus függvények 165
8.1.3 Néhány fontosabb tétel 165
8.2 Szimmetrikus függvények indentifikációja, szimmetria változók kijelölése 166
8.3 Szimmetrikus függvényeket realizáló reiteratív struktúrájú
kombinációs hálózatok 173
8.4 Pozicionális hálózatok 177
8.5 Hid struktúrák 178
8.5.1 Közvetlen összeköttetési táblázat 179
8.5.2 Topológiai módszer 180
9. fejezet 181
KÜSZÖB-LOGIKÁS HÁLÓZATOK 181
9.1 Bevezető fogalmak 181
9.2 Egyszerű és összetett küszöb függvények 184
9.3 Küszöb függvényekkel kapcsolatos fontosabb tételek 184
9.4 Geometriai reprezentálás és lineáris szeparálhatóság 185
9.5 Egyszerű küszöbfüggvények identifikációja 187
9.6 Összetett küszöbfüggvényes szintézis Veitch-Karnaugh táblák
segítségével 192
9.7 Néhány megjegyzés 196
9.8 Majoritás és minoritás logikák 198
10. fejezet 200
TÖBBÉRTEKŰ LOGIKÁK
10.1 A Post függvény fogalma 200
10.2 Operációk, komplemens, algebra 200
10.3 Term. táblák 202
10.4 Minimalizálás 208
10.4.1 Formuláris módszerek 208
10.4.2 Grafikus módszerek 211
10.5 Megjegyzések, realizációs kérdések 211
11. fejezet 217
HAZARDOK
11.1 Logikai hazardok 217
11.1.1 Sztatikus hazard 218
11.1.2 Dinamikus hazard 221
11.1.3 A logikai hazard hasznosítása 221
11.1.4 Logikai hazardok kiküszöbölése 222
11.1.5 Részben határozott hálózatok problémája hazard
kiküszöbölésnél 223
11.1.6 Dekompoziciós hálózatok hazard kérdése 224
11.2 Funkcionális hazard 224
11.3 Lényeges hazard 226
12. fejezet 227
LOGIKAI EGYENLETEK, EGYENLETRENDSZEREK ÉS EGYENLŐTLENSÉGEK
12.1 Alapvető definíciók és összefüggések 228
12.2 Szisztematikus megoldási módszerek 229
12.2.1 Algebrai módszer 230
12.2.2 Előzetes megkötöttség 233
12.2.3 Grafikus módszer 234
13. fejezet 247
KOMBINÁCIOS HÁLÓZATOKBÓL FELÉPÜLŐ FUNKCIONÁLIS
EGYSÉGEK 247
13.1 Kód konverterek 247
13.2 Szelektorok és demultiplexerek 252
13.3 Komparátorok 253
13.4 Aritmetikai műveletvégzők 254
13.5 Ellenőrzők 255
14. fejezet 257
SZEKVENCIÁLIS HÁLÓZATOK, MINT ABSZTRAKT AUTOMATÁK I.
14.1 Szekvenciális hálózat, mint automata 259
14.2 Automaták csoportosítása 265
14.3 Automatáknál alkalmazott leírásmódok 265
14.3.1 Idő és ütemdiagramok 266
14.3.2 Irányított gráf 267
14.3.3 Huffman tábla 269
14.3.4 Mátrixos leírás 270
14.4 Transzformációk a Mealy és Moore modellek között 281
14.4.1 Moore Mealy irányú transzformáció 281
14.4.2 Mealy Moore irányú transzformáció 282
15. fejezet 287
SZEKVENCIÁLIS HÁLÓZATOK, MINT ABSZTRAKT AUTOMATÁK II.
15.1 Néhány fontosabb speciális automata 287
15.2 A felépítési struktúra néhány kérdése 288
15.2.1 Automaták összekapcsolása 288
15.2.2 Néhány meggondolás 292
15.3 Aszinkron és szinkron rendszerek 294
15.4 Az analízissel és szintézissel kapcsolatos alapvető meggondolások 296
15.4.1 Automata-leképezés, analízis, szintézis 296
15.4.2 Ekvivalencia, lefedés, kompatibilitás 297
16. fejezet 300
ASZINKRON HÁLÓZATOK ALAPFOGALMAI. TÁROLÓELEMEK
16.1 Előzetes meggondolások és alapfogalmak 300
16.1.1 Stabil, instabil működési állapot 300
16.1.2 Jellemző táblák 301
16.1.3 Versenyfutási jelenségek 305
16.1.4 Lényeges hazard 306
16.1.5 Hálózatelméleti meggondolások 307
16.1.6 Felépítési módozatok
16.1.7 A működéssel kapcsolatos korlátozások és
meggondolások 308
16.2 Tárolóelemek 309
16.2.1 Alaptípusok 309
16.2.2 Tárolóelemek realizációs kérdései 314
17. fejezet 323
SZINKRON HÁLÓZATOK SZINTÉZISÉ
17.1 Alaptulajdonságok és néhány meggondolás 323
17.2 Előre behatárolt struktúrájú szinkron hálózatok tervezése az
állapotegyenlet megoldásával 325
17.2.1 Bevezető példa 325
17.2.2 Az eljárás algoritmusa 330
17.3 Az állapottábla egyszerűsítésén alapuló eljárás 333
17.3.1 Egyértelmű jellemzés állapotdiagram 335
17.3.2 Az állapottábla egyszerűsítése teljesen meghatározott
hálózat esetén 337
17.3.3 Az állapottábla egyszerűsítése részben meghatározott
hálózat esetén 343
17.3.4 Allapotkódolás 346
17.3.5 Az eljárás további menete 352
18. fejezet 353
ASZINKRON HÁLÓZATOK SZINTÉZISE
18.1 Klasszikus intuitív eljárás 353
18.1.1 Bevezető példa 353
18.1.2 Az eljárás algoritmusa 357
18.1.3 Magyarázó példák 359
18.2 A primitív állapottábla egyszerűsítésén alapuló eljárás 367
18.2.1 Bevezető példa 367
18.2.2 Az eljárás algoritmusa 373
18.2.3 Szemléltető összetett példa 378
19. fejezet 393
SZEKVENCIÁLIS HÁLÓZATOKBÓL FELÉPÜLŐ FUNKCIONÁLIS
EGYSÉGEK
19.1 Regiszterek 393
19.2 Sorozatszürők. Lineáris automaták 396
19.3 Számlálók 401
19.4 Frekvencia osztók 404
19.5 Memóriák 404
20. fejezet 407
LOGIKAI RENDSZEREK HIBA ANALÍZISÉVEL KAPCSOLATOS
ALAPOK
20.1 Hibás működés, diagnosztizálás
20.2 A diagnosztizálással kapcsolatos alapvető módszerek és fogalmak összefoglalása 408
20.3 Az ekvivalens normál alak és vele kapcsolatos meggondolások 413
20.3.1 Származtatás 413
20.3.2 Hibadetektálás az ekvivalens normál alak felhasználásával 415
20.4 Egy összetett analízis algoritmusa 416
IRODALOMJEGYZÉK 418
Dr. Szittya Ottó
Dr. Szittya Ottó műveinek az Antikvarium.hu-n kapható vagy előjegyezhető listáját itt tekintheti meg: Dr. Szittya Ottó könyvek, művekMegvásárolható példányok
Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.