1.066.801
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát

VISSZA
A TETEJÉRE
JAVASLATOKÉszre-
vételek
Irányítási rendszerek elmélete és tervezése I.
Egyváltozós szabályozások
| Kiadó: | Akadémiai Kiadó |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Ragasztott papírkötés |
| Oldalszám: | 491 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 24 cm x 17 cm |
| ISBN: | 963-057-787-9 |
| Megjegyzés: | Fekete-fehér ábrákkal illusztrált. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Előszó
Az irányítástechnika a műszaki tudományoknak azon ága, amely a különféle (műszaki, biológiai, közgazdasági stb.) területeken az irányítási műveletek általános törvényszerűségeivel, vizsgálati... TovábbElőszó
Az irányítástechnika a műszaki tudományoknak azon ága, amely a különféle (műszaki, biológiai, közgazdasági stb.) területeken az irányítási műveletek általános törvényszerűségeivel, vizsgálati módszereivel és az irányítások tervezésével és realizálásával foglalkozik. Az irányítástechnika elengedhetetlen alapját képezi a technikai fejlődésnek, nélküle nem hozhatók létre biztonságos erőművi rendszerek, robotizált gyártórendszereknek, repülőgépek és űrtechnikai berendezések. A könyv a Budapesti Műszaki és Gazdaságtudományi Egyetem (korábban Budapesti Műszaki Egyetem) Villamosmérnöki és Informatikai Karán „Szabályozástechnika" címmel 1992-től tartott előadásaimon alapul, melyek a műszaki informatika szakon hangzottak el. A három kötetre tervezett sorozat eme első kötete az irányítási rendszerek elméletének és tervezési módszereinek klasszikus és modern irányzatait tárgyalja szigorú, de logikusan felépített szemléletben és egységes rendszertechnikai látásmódot közölve. Bevezetőjében összefoglalja az irányítástechnikai alapfogalmakat, az irányításelmélet főbb irányzatait, az irányítások tervezésének főbb lépéseit és az irányítások dinamikus és integrális minőségi jellemzőit. Ezután először általános rendszertechnikai összefoglalót ad a folytonosidejű és diszkrétidejű rendszerekről, a rendszerek különféle leírásairól többváltozós (multi inputmulti output, MIMO) rendszerek esetén, és bemutatja a dinamikus rendszerek szimulációjának fontosabb numerikus módszereit (Euler, Runge-Kutta és Adams módszerek). A folytonos és diszkrétidejű rendszerek tárgyalásának módja lehetőséget ad az algebrai hasonlóságok kiemelésére. Bemutatja a nemlineáris rendszerek stabilitásvizsgálati módszereit (Ljapunov direkt és indirekt módszere, LaSalle tétel), a nemlineáris rendszer linearizálását egyensúlyi állapot közelében, és a klasszikus (pólusokon, sajátértékeken alapuló) és a Ljapunov-féle stabilitás közötti kapcsolatot lineáris időinvariáns rendszerek esetén. Módszereket ad az egyváltozós (single input-single output, SISO) folytonosidejű lineáris rendszerek követési tulajdonságainak jellemzésére és stabilitás vizsgálatára (argumentum elv, Hurwitz, Nyquist és Bode stabilitáskritériumok). Bemutatja a zárt rendszer dinamikus minőségi jellemzői és a domináns konjugált komplex póluspár közötti összefüggéseket. Megadja a PID szabályozók jellemzését idő és frekvencia tartományban. Módszert ad a szabályozóbeállítás tervezésére előírt statikus pontosság, fázistöbblettel jellemzett stabilitástartalék és a szabályozó kimenő jelére előírt korlátozás esetén. Bemutatja a holtidős rendszerek szabályozási módszereit, közöttük a Smith prediktort. Ismerteti a gyökhelygörbe módszert a körerősítés megválasztására. Ezután rátér a diszkrétidejű (mintavételes) szabályozások tervezésére. Először bemutatja a matematikai mintavételezés Shannon tételét, az analóg jel rekonstrukcióját a mintákból, és az ideális aluláteresztő szűrő közelítését tartószervekkel. Ökölszabályt ad a mintavételi idő megválasztására. Módszert ad a folytonos-diszkrét áttérésre frekvenciatartományban és állapottérben. Bemutatja a mintavételes rendszerek stabilitáskritériumait (Jury, Nyquist, Bode). Bemutatja az analóg szabályozók mintavételes közelítésének módszereit, a mintavételes PID szabályozó realizálását és az integrátor antiwindup korrekciót telítéssel rendelkező beavatkozó szerv esetén. VisszaTartalom
Előszó 11Jelölések 13
1. Bevezetés 17
1.1 Irányítástechnikai alapfogalmak 17
7.2 Szabályozások minőségi jellemzői 24
1.3 Szabályozások osztályozása 26
1.4 Szabályozási rendszerek tervezésének lépései 27
1.5 A szabályozáselmélet főbb irányzatai 28
1.6 A könyv felépítése 30
2. Dinamikus rendszerek 35
2.1 Dinamikus rendszerek definíciója 35
2.2 Dinamikus rendszerek osztályozása 37
3. Folytonosidejű lineáris dinamikus rendszerek 41
3.1 Folytonosidejű időben változó lineáris rendszerek 41
3.2 Folytonosidejű időinvariáns lineáris rendszerek 43
3.3 Példa lineáris rendszerre: egyenáramú motor 49
4. Diszkrétidejű lineáris dinamikus rendszerek 53
4.1 Diszkrétidejű időben változó lineáris rendszerek 53
4.2 Diszkrétidejű időinvariáns lineáris rendszerek 55
5. Folytonosidejű nemlineáris rendszerek 59
5.1 Numerikus módszerek az állapotegyenlet megoldására 59
5.2 Nemlineáris rendszer perturbációja és linearizálása 62
5.3 Példák nemlineáris rendszer dinamikus modelljének meghatározására 64
5.3.1 Lejtőn guruló golyó modellje 66
5.3.2 Az invertált inga dinamikus modellje 68
5.3.3 Kétszabadságfokú robotkar dinamikus modellje 70
5.4 Nemlineáris rendszerek stabilitása 73
6. Folytonosidejű lineáris szabályozások analízise 85
6.1 Lineáris tagok és rendszerek leírási módszerei 85
6.2 Alaptagok, alapkapcsolások 89
6.2.1 Alapkapcsolások, szabályozási kör, felnyitott kör 89
6.2.2 Alaptagok 92
6.2.3 Szabály a felnyitott kör aszimptotikus amplitúdó-jelleggörbéjének felrajzolására
6.3 Kapcsolat a domináns pólus és a dinamikus minőségi jellemzők között 102
6.4 Lineáris szabályozások állandósult állapota 105
6.4.1 Alapjelkövetés 106
6.4.2 Zavaró jel kompenzálás 108
6.5 Stabilitási kritériumok 110
6.5.1 Hurwitz-féle stabilitási kritérium 110
6.5.2 Nyquist-féle stabilitási kritérium 113
6.5.3 Bode-féle stabilitási kritérium 119
6.6 A stabilitási tartalék jellemzése fázistöbblettel 122
7. Folytonosidejű lineáris szabályozások tervezése 125
7.1 PID típusú szabályozók 125
7.1.1 Ideális PID szabályozó 126
7.1.2 Közelítő PID szabályozó 129
7.2 Szabályozó beállítás tervezése előírt statikus pontosság és fázistöbblet esetén 131
7.2.1 Kompenzálás P szabályozóval 133
7.2.2 Kompenzálás PD szabályozóval 134
7.2.3 Kompenzálás Pl szabályozóval 136
7.2.4 Kompenzálás PID szabályozóval 137
7.2.5 Visszacsatolásos kompenzálás 140
7.3 Szabályozó beállítás tervezése a hibanégyzet-integrál minimalizálásával 142
7.4 Gyökhelygörbe módszer 147
7.4.1 Gyökhelygörbe rajzolási szabályok pozitív erősítés esetén 147
7.4.2 Gyökhelygörbe rajzolási szabályok negatív erősítés esetén 152
7.5 Holtidős tagot tartalmazó rendszerek irányítása 153
7.5.1 Holtidős tagot tartalmazó rendszer jelátviteli tulajdonságai 153
7.5.2 Holtidős tag közelítése Padé-sorfejtéssel 155
7.5.3 Ideális holtidős tag szabályozása 156
7.5.4 Holtidős rendszer szabályozása Smith-prediktorral 159
7.6 Szabályozó beállítás tervezése a beavatkozó jelre előírt korlátozás esetén 160
7.6.1 Statikus pontosság 161
7.6.2 Kompenzálási stratégia 162
7.6.3 A maximális beavatkozó jelre vonatkozó feltétel kapcsolata a szabályozó átmeneti függvényével 163
7.6.4 A felnyitott kör frekvenciafüggvényére vonatkozó feltételek 164
7.6.5 A tervezési feltételek megfogalmazása nemlineáris egyenletrendszer alakjában 165
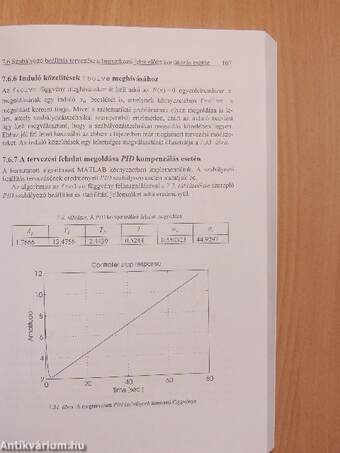
7.6.6 Induló közelítések fsolve meghívásához 167
7.6.7 A tervezési feladat megoldása PID kompenzálás esetén 167
7.7 Példa háromhurkos kaszkádszabályozás tervezésére 169
7.7.1 A belső áramszabályozási hurok megtervezése 170
7.7.2 A középső sebességszabályozási hurok megtervezése 172
7.7.3 A külső pozíciószabályozási hurok megtervezése 173
7.8 Szabályozók kísérleti beállítása 175
7.8.1 Ziegler-Nichols-szabály 176
7.8.2 Janssen-Offereins-szabály 176
7.8.3 Oppelt- és Chien-Hrones-Reswick-módszer 177
7.8.4 Strejc-módszer 179
7.8.5 Reinisch-módszer 183
8. Diszkrétidejű lineáris szabályozások analízise 187
8.1 Shannon-féle mintavételezési törvény 187
8.2 Tartószervek 192
8.3 Jelterjedés leírása mintavételezett rendszerekben frekvenciatartományban. 195
8.4 A jelterjedés leírása mintavételezett rendszerekben állapottérben 201
8.4.1 Lineáris tag diszkrétidejű állapotegyenlete lépcsős bemenet esetén 201
8.4.2 Holtidős lineáris tag diszkrétidejű állapotegyenlete lépcsős bemenet esetén 203
8.5 Analóg kompenzáló tagok mintavételes implementálása 205
8.5.1 Differenciáló és integráló operátorok mintavételes közelítése 205
8.5.2 Analóg tag mintavételes ekvivalense rögzített bemenőjel esetén 207
8.5.3 A mintavételes közelítés megvalósítása 208
8.5.4 PID szabályozó mintavételes megvalósítása 209
8.6 A domináns póluspár helye a z-síkon 213
8.7 Mintavételes rendszerek stabilitása 214
8.7.1 Jury-féle stabilitási kritérium 214
8.7.2 Nyquist-féle és Bode-féle stabilitási kritériumok 216
8.8 Példa analóg PID szabályozó mintavételes megvalósítására 217
9. Diszkrétidejű lineáris szabályozások tervezése 221
9.1 Mintavételes szabályozás tervezése bilineáris transzformációval 222
9.1.1 A bilineáris transzformáció hatása a pólusokra és a zérus helyekre 223
9.1.2 Szabályozó beállítás tervezése korlátozott beavatkozó jel esetén 225
9.1.3 Példa bilineáris transzformációval történő szabályozás tervezésére 226
9.2 Véges beállási idejű (dead-beat) szabályozás 229
9.2.1 Tervezési előírások és megvalósításuk 229
9.2.2 A zárt rendszer pólusai dead-beat szabályozás esetén 230
9.2.3 A korrekciós polinom méretezése 231
9.2.4 A mintavételi idő megválasztása aperiodikus tranziens és bemenőjel korlátozás esetén 232
9.2.5 Példa véges beállási idejű szabályozás tervezésére 233
9.3 Két szabadságfokú mintavételes szabályozás tervezése 235
9.3.1 Referencia modell és megfigyelő polinom 236
9.3.2 A tervezés visszavezetése diophantoszi egyenletre 237
9.3.3 Kauzalitási feltételek konvertálása fokszám feltételekké 239
9.3.4 Kétszabadságfokú szabályozás tervezési algoritmusa 240
9.3.5 A paraméterváltozások hatása 244
9.3.6 Példa kétszabadságfokú szabályozó tervezésére 245
9.3.7 Modell-követő szabályozás 248
9.3.8 A módszer általánosítási lehetőségei 249
9.3.9 Példa aktív csillapításra 253
9.4 Holtidős rendszer mintavételes szabályozása Smith-predikt orral 255
9.4.1 Smith-prediktor mintavételes realizálása 255
9.4.2 Példa holtidős rendszer Smith-prediktorral történő szabályozására 257
10. Irányíthatóság és megfigyelhetőség 261
10.1 Folytonosidejű lineáris rendszerek irányíthatósága 262
10.1.1 Az irányíthatóság és elérhetőség feltételei időben változó lineáris rendszerek esetén 263
10.1.2 Az irányíthatóság és elérhetőség feltételei időinvariáns lineáris rendszerek esetén 265
10.1.3 Lineáris időinvariáns rendszer irányíthatósági lépcsős alakja 269
10.2 Folytonosidejű lineáris rendszerek megfigyelhetősége 271
10.2.1 A megfigyelhetőség és rekonstruálhatóság feltételei időben változó lineáris rendszerek esetén 272
10.2.2 A megfigyelhetőség és irányíthatóság dualitása időinvariáns lineáris rendszerek esetén 274
10.3 Folytonosidejű lineáris rendszerek Kalman-féle felbontása 278
10.4 Diszkrétidejű rendszerek irányíthatósága és elérhetősége 280
10.5 Diszkrétidejű rendszerek megfigyelhetősége és rekonstruálhatósága 282
10.6 Pólus áthelyezés és állapotmegfigyelés diszkrét időben 284
11. Szabályozások tervezése állapottérben 287
11.1 Folytonosidejű szabályozások tervezése állapottérben 288
11.1.1 Pólusáthelyezés állapot-visszacsatolással 288
11.1.2 Ackermann-képlet 289
11.1.3 Állapot-visszacsatolás realizálása megfigyelővel 291
11.1.4 Alapjel miatti korrekció folytonos időben 292
11.1.5 Integráló szabályozás 293
11.1.6 Terhelésbecslés 294
11.1.7 Pólus/zérus kiejtés állapot-visszacsatolás, megfigyelő és alapjel miatti korrekció együttes alkalmazásakor 296
11.1.8 Példa folytonosidejű szabályozás tervezésére állapottérben 297
11.2 Diszkrétidejű szabályozások tervezése állapottérben 305
11.2.1 Pólusáthelyezés állapot-visszacsatolással 305
11.2.2 Állapot-visszacsatolás realizálása aktuális megfigyelővel 306
11.2.3 Alapjel miatti korrekció diszkrét időben 308
11.2.4 Integráló szabályozás 309
11.2.5 Terhelésbecslés 311
11.2.6 Példa diszkrétidejű szabályozás tervezésére állapottérben 312
12. Optimalizálás és paraméterbecslés 331
12.1 Az optimum analitikus feltételei 331
12.1.1 Az optimum analitikus feltételei függvényterekben 333
12.1.2 Az optimum analitikus feltételei részben rendezett terekben 336
12.1.3 Optimalizálási problémák az irányítástechnikában 339
12.2 Optimum kereső eljárások végesdimenziós terekben 341
12.2.1 Optimum keresés egy skalárváltozóban 341
12.2.2 Gradiens módszer 343
12.2.3 Konjugált gradiens módszer 343
12.2.4 Newton-módszer 347
12.2.5 Gradienshez hasonló eljárások 348
12.3 Lineáris paraméterbecslés 350
12.3.1 Lineáris paraméterbecslés batch-üzemmódban 351
12.3.2 Rekurzív lineáris paraméterbecslés 351
12.4 Nemlineáris paraméterbecslés lokális linearizálással 359
12.5 Függvény-approximáció soft computing technikákkal 360
12.5.1 Függvény-approximáció többrétegű neurális hálózattal 360
12.5.2 Függvény-approximáció Sugeno-féle fuzzy rendszerrel 366
12.5.3 Példa nemlineáris rendszer modellezésére Sugeno-féle fuzzy rendszerrel 369
13. Diszkrétidejű lineáris rendszerek identifikációja 373
13.1 A kimenő jel optimális predikciója 373
13.2 Tipikus diszkrétidejű rendszer modellek 376
13.3 Identifikáció és paraméterbecslés kapcsolata 381
13.3.1 ARX modell identifikációja a legkisebb négyzetek módszerével 383
13.3.2 ARX modell identifikációja a segéd változók módszerével 386
13.3.3 ARMAX modell identifikációja 389
13.3.4 PEM modell identifikációja 390
13.4 Többváltozós rendszer altér-bázisú identifikációja 393
13.4.1 Elméleti alapok 393
13.4.2 A közönséges MOESP módszer 395
13.5 Példák lineáris rendszerek identifikációjára 401
13.5.1 Példa ARMAX és IV4 módszerrel történő identifikációra 401
13.5.2 Példa a MOESP módszerrel történő identifikációra 406
Függelék 415
F1. Vektor és mátrix algebra 415
F1.1 Alapfogalmak 415
F1.2 Gram-Schmidt ortogonalizáció 420
F1.3 Sajátérték, sajátvektor, Jordan-alak 422
F1.4 Leverrier-Faddajeva-algoritmus 424
F2. Komplex függ vény tani alapok 425
F2.1 Komplex szám, komplex függvény, regularitás 425
F2.2 Taylor-sor, Laurent-sor, reziduum tétel 426
F2.3 Argumentum elv 427
F3. Fourier- és Laplace-transzformált 429
F3.1 Fourier-sor, diszkrét spektrum 429
F3.2 Fourier-transzformált, inverz Fourier-transzformált 430
F3.3 Laplace-transzformált, inverz Laplace-transzformált 432
F3.4 Tipikus függvények Laplace-transzformáltjai 434
F3.5 Az inverz Laplace-transzformált meghatározása 434
F3.6 Lineáris differenciálegyenlet megoldása 435
F4. Z-transzformált 439
F4.1 A Z-transzformált definíciója és tulajdonságai 439
F4.2 Tipikus sorozatok Z-transzformáltjai 440
F5. Mintavételezett rendszerek átviteli függvényei 443
F5.1 Másodrendű rendszerek diszkrétidejű átviteli függvényei 443
F5.2 Harmadrendű rendszerek diszkrétidejű átviteli függvényei 446
F6. Stabil lineáris operátorok a sorozatok l2 terében 451
F6.1 A végtelen sorozatok U tere 451
F6.2 Korlátos (stabil) operátorok és inverzük a végtelen sorozatok U terében 451
F7. A sztochasztikus folyamatok alapjai 453
F7.1 Valószínűségszámítási alapok 453
F7.2 A sztochasztikus folyamatok alapjai 455
F7.3 Mozgóátlagy autoregresszív és Markov-folyamatok 457
F7.4 Lineáris sztochasztikus differenciaegyenlet 458
F7.5 Lineáris rendszer válasza sztochasztikus bemenő jelre 459
F7.6 Innovációs reprezentáció 461
F7.7 A zajmodell normalizálása 462
F8. MATLAB, Simulink, Toolboxok 465
F8.1 A MATLAB környezet általános jellemzése 465
F8.2 Bevezetés a MATLAB és a Control System Toolbox használatába 468
F8.2.1 MATLAB alapok - a parancs ablak (command window) 468
F8.2.2 A MATLAB grafikus lehetőségei 473
F8.2.3 Ábra hozzáférhetővé tétele más alkalmazások számára 476
F8.2.4 Az .m kiterjesztésű állományok 476
F8.2.5 A MATLAB programozási nyelve 477
F8.2.6 Saját függvények létrehozása MATLABbal 477
F8.3 A Control System Toolbox 479
F8.4 Simulink 485
Irodalomjegyzék 489
Lantos Béla
Lantos Béla műveinek az Antikvarium.hu-n kapható vagy előjegyezhető listáját itt tekintheti meg: Lantos Béla könyvek, művekMegvásárolható példányok
Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.