Korszerű szabályozáselmélet

Nemlineáris, optimális és adaptív rendszerek

Szerző

Csáki Frigyes

Szerkesztő

Horváth Ferenc

Budapest

'Csáki Frigyes: Korszerű szabályozáselmélet ' összes példány

Kiadó:	Akadémiai Kiadó
Kiadás helye:	Budapest
Kiadás éve:	1970
Kötés típusa:	Fűzött keménykötés
Oldalszám:	1.085 oldal
Sorozatcím:
Kötetszám:
Nyelv:	Magyar
Méret:	25 cm x 17 cm
ISBN:
Megjegyzés:	A könyv fekete-fehér ábrákkal illusztrált.

Értesítőt kérek a kiadóról

A beállítást mentettük,
naponta értesítjük a beérkező friss
kiadványokról

Tartalom

Jelölések	23
Előszó	37
Irodalom	39
Bevezetés	43
A nemlineáris rendszerek sajátosságai	43
A nemlineáris rendszerek jelentősége	43
Alapösszefüggések	43
Állapotegyenletek, fázisegyenletek	46
A nemlineáris rendszerek néhány különleges tulajdonsága	48
A nemlinearitások osztályozása	50
A nemlineáris rendszerek elemzésére használt módszerek	52
Irodalom	52
Linearizálási módszerek	57
A munkaponti linearizálás módszere	58
A linearizált paraméterek meghatározása sorbafejtéssel	58
A linearizálás gyakorlati módszere	64
A linearizálás leggyakrabban használt algebrai közelítései	66
A jelleggörbék linearizálása	68
A linearizált együtthatók meghatározása a legkisebb négyzetes hibák módszerével	69
A Ljapunov-féle első stabilitásvizsgálati módszer	73
Összefoglalás	78
Irodalom	79
A harmonikus linearizálás	80
A leíró függvény módszer alapfeltevései	81
Alapösszefüggések	89
Általánosított leíró függvények	90
Néhány egyszerűbb nemlinearitás leíró függvénye	98
A leíró függvény közelítő meghatározása	102
Egy másik közelítő módszer a leíró függvények meghatározására	105
Stabilitásvizsgálat	115
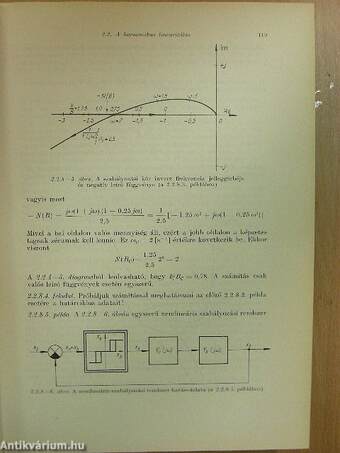
Példák a leíró függvények használatára	121
A nemlineáris rendszer gyök-helygörbéje	126
A leíró függvény módszer hibái	130
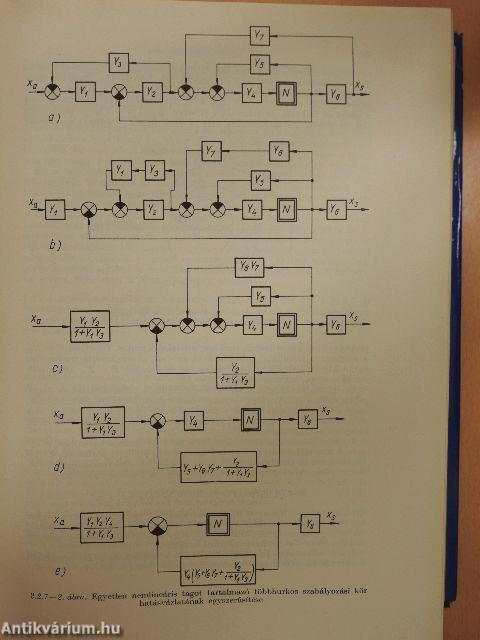
Kompenzálás nemlineáris rendszerekben	132
A harmonikus egyensúly módszere	132
Az állapotegyenletek harmonikus linearizálása	133
A három módszer összehasonlítása	135
Egyéb leíró függvények	137
A fordított feladat	139
A statisztikus linearizálás	148
Alapösszefüggések	148
A nemlineáris jelleggörbék statisztikus linearizálása	152
A linearizált átviteli tényezők kiszámítása	154
Példák a statisztikus átviteli tényezők meghatározása	159
A linearizált átviteli tényezők kiszámításának egy változata	168
Néhány jellegzetes nemlinearitás statisztikus linearizálása	169
Statisztikus rendszerelemzés	174
Irodalom	180
Együttes leíró függvények	183
A kettős leíró függvény	183
A növekmény helygörbe	186
A közelítő kettős leíró függvény	190
Együttes harmonikus és statisztikus linearizálás	194
Az együttes linearizálás képleteinek összefoglalása	197
Közelítő együttes linearizálás	199
Irodalom	200
Az átmeneti folyamatok meghatározása	205
Grafikus módszerek	206
Egytárolós lineáris tag	206
Lineáris integráló tag	209
Egytárolós nemlineáris tag	210
Visszacsatolt szabályozási rendszerek	211
Kiegészítő megjegyzések	214
A szekáns módszer	215
Kiegészítő megjegyzések a szekáns módszerhez	217
A tangens módszer	221
Irodalom	223
Numerikus módszerek	224
A Taylor-sorba fejtés	224
Az Euler-módszer	227
A módosított Euler-módszer	228
Az Adams-módszer	229
A Milne-módszer	231
A Runge-Kutta-módszer	232
Prediktor-korrektor módszerek	234
A numerikus módszerek ellenőrzése	238
A legkisebb négyzetes hibák módszere	239
A z-alakok felhasználása az átmeneti folyamat kiértékeléséhez	241
Naumov grafo-analitikus módszere	244
Analitikus módszerek	249
Az állandók variálása	250
Sorbafejtés kis paraméter szerint	253
A kis paraméter szerinti sorbafejtés különleges esete	256
Periodikus megoldások meghatározása a perturbációs módszerrel	258
A visszaszármaztatási módszer	261
Lighthill és Temple módszere	262
Az egyeztetések (a kollokáció) módszere	265
Galerkin módszere	268
Ritz-Galerkin módszere	270
A Lie-sor módszere	272
Az aszimptotikus sorok módszere	274
A Taylor-Cauchy-transzformáció	275
A rekurziós módszer	277
A komplex konvolúció módszere	279
A sorozatos integrálás módszere	282
A Lalesco-féle nemlineáris integrálegyenletek	283
Irodalom	286
Zárt megoldású átmeneti folyamatok	287
Közvetlenül integrálható differenciálegyenletek	287
Elsőrendű linerális differenciálegyenletek	288
Szétválasztható differenciálegyenletek	289
Homogén változó bevezetése	290
A teljes differenciálból származó egyenlet megoldása	291
Integráló tényező bevezetése	292
Új változó bevezetése	292
Kihagyásos másodrendű differenciálegyenletek	292
A Bernoulli-egyenlet	293
A Riccati-egyenlet	294
Az Euler-Cauchy-egyenlet	295
A változó együtthatós lineáris differenciálegyenletek megoldása	295
Elliptikus függvények	296
Hiperelliptikus függvények	300
Irodalom	301
Az állapotsík és a fázissík módszer	305
Az állapotsík és a fázissík módszer alapjai	306
A fázisegyenletek megállapítása	308
A fázisportré meghatározása számítással	312
Grafikus módszerek a fázistrajektóriák megszerkesztésére	323
Az evolúta módszerek	333
Az idő meghatározása a fázistrajektóriákon	339
A szinguláris pontok Poincaré-féle vizsgálata	343
Kiegészítő megjegyzések a Poincaré-módszerhez	359
Az energia leolvasása a fázisportréból	361
A fázistrakektóriák megszerkesztése az energiaszemlélet alapján	363
A határciklus vizsgálata	366
Szakaszonként lineáris rendszerek	374
Telítés, illetve korlátozás	374
Értéketlenségi sáv	377
Változó erősítés	378
Kotyogás, illetve hiszterézis	381
Tapadás és szárazsúrlódás	384
Változó csillapítás	387
A szakaszonként lineáris rendszerek vizsgálata	389
Irodalom	391
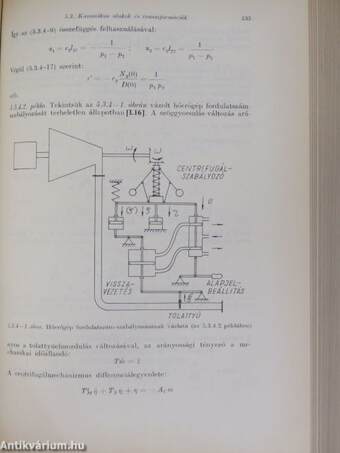
Állásos szabályozás	393
Az állásos szabályozás hatásvázlata	395
A fázistraketóriák számítása	396
Néhány példa az állásos szabályozásokra	400
A jelleggörbék módszere	408
A ponttranszformáció módszere	411
A határciklus-számítás relés rendszerekben	419
Optimális relés szabályozások	426
Minimális áttérési idejű rendszerek	435
Irodalom	443
A nemlineáris rendszerek stabilitása	449
Ljapunov második, közvetlen módszere	451
A stabilitás alapfogalmai	452
Az előjel-határozottság fogalma	456
A Ljapunov-függvény fogalma	458
Ljapunov tételei	460
Példák a Ljapunov-módszer alkalmazására autonóm rendszerekben	465
A Ljapunov-módszer bizonyítása	475
A Ljapunov-módszer alkalmazása nemautonóm rendszerekre	479
A gyakorlati stabilitás	481
Az esetleges stabilitás	482
A Ljapunov-függvények meghatározása	486
A Ljapunov-függvények meghatározása autonom lineáris rendszerekre	486
A Ljapunov-függvények meghatározása autonóm nemlináris rendszerekre	489
Kraszovszkij módszere	494
Ajzerman módszere	497
A változó gradinse módszer Ljapunov-függvények előállítására	499
Zubov módszere	503
A Ljapunov-függvények meghatározása nemautonóm rendszerekre	506
Irodalom	508
Kanonikus alakok transzformációk	509
A közvetlen szabályozás alapegyenletei	513
A közvetett szabályozás alapegyenletei	520
Zárt képletek a kanonikus transzformációra közvetlen szabályozáskor	528
Zárt képletek a kanonikus transzformációra közvetett szabályozáskor	530
A Ljapunov-függvény megválasztása. Előkészítő megjegyzések	535
A Ljapunov-függvény megválasztása közvetett szabályozáskor	536
A Ljapunov-függvény megválasztása közvetlen szabályozáskor	544
A Lurje-féle polinomtranszformáció	546
A Lurje-féle polinomtranszformáció speciális esetei	554
Egyszerűsített stabilitási kritériumok	557
A póluseltolás és a zérushelyeltolás	560
Irodalom	567
Méretezés a Ljapunov-módszer alapján	568
Méretezés az integrálkritérium alapján	570
Zárt szabályozási rendszernek méretezése	571
A nemlineáris gerjesztett rendszer méretezése	573
A paraméter-identifikációs módszer	575
A nemlineáris adaptív szabályozó méretezése	577
Az aszimptotikusan stabilis optimális nemlineáris rendszerek méretezése	579
Az átmeneti folyamat csillapodási sebességének becslése	584
Mintavételező rendszerek	591
Stabilitási fogalmak	591
Stabilitási tételek	592
A Routh-Hurwitz-kritérium és a Ljapunov-módszer kapcsolata	597
Kraszovjszkij módszere szaggatott működésű rendszerekre	598
A szaggatott működésű rendzserek méretezése	602
Az átmeneti folyamat becslése	603
Irodalom	604
Az abszolút stabilitás	605
Az abszolút stabilitás fogalma	606
A Popov-kritérium és bizonyítása	608
A Popov-kritérium geometriai értelmezése	612
A Popov-kritérium kiterjesztése	616
Példák a Popov-kritérium használatára	619
A nemlineáris rendszerek szabályozási folyamatának abszolút stabilitása	626
A nemlineáris rendszerek stabilitási foka	628
A nemlineáris rendszerek integrálkritériuma	630
A Popov-módszer és a Ljapunov-módszer kapcsolata	631
A nemlináris szaggatott működésű rendszerek abszolút stabilitása	633
Az abszolút stabilitás szaggatott működésű rendszerre	633
A Popov-kritérium értelmezése	637
A stabilitási kritérium általánosítása	638
Az abszolút stabilitás szükséges és elégséges feltételei	639
A stabilitás fokának becslése	639
A kvadratikus becslés	640
Kapcsolat a Popov-kritérium és Ljapunov-módszer között, szaggatott működésű szabályozási rendszer esetén	641
A frekvenciamódszer néhány általánosítása	643
A korlátozott meredekségű nemlineáris tagot tartalmazó rendszerek abszolút stabilitása	645
Módosított stabilitási kritériumok a frekvenciatartományban	650
A többváltozós rendszerek abszolút stabilitása	653
Az időben változó nemlinearitás tekintetbevétele	657
Irodalom	658
Optimális rendszerek	667
A variációszámítás felhasználása optimális irányítási feladatok megoldására	669
A klasszikus variációszámítás néhány tétele	669
Optimális irányítási feladatok változatai	686
A mozgó végpontú autonóm rendszerek optimális irányítása	697
Lineáris optimalizálási feladatok	700
Irodalom	710
A Pontrjagin-féle elv	713
A Pontrajagin-féle maximum elv	713
Néhány példa a maximum-elvre	732
A Pontrjagin-féle minimum-elv	740
A lineáris, autonóm szabályozott szakaszok optimális irányítása	749
Az optimális rendszerek néhány sajátsága	755
A minimális idejű rendszerek méretezése	767
A minimális hajtóanyag-felhasználású optimális rendszerek méretezése	825
A minimális energiájú optimális irányítások	835
Az hipergömb által korlátozott optimális irányítások	841
Irodalom	851
A dinamikus programozás	862
A dinamikus programozás alapjai	862
A dinamikus programozás és a minimum- (illetve maximum) elv kapcsolata	873
A dinamikus programozás és a variációszámítás kapcsolata	876
Kapcsolat a Ljapunov-függvények és a dinamikus programozás között	879
Irodalom	883
A funkcionálanalízis felhasználása az optimális irányítási feladatok megoldásához	885
Az egyváltozós szabályozott szakaszok optimális irányítása	885
A többváltozós szabályozott szakaszok optimális irányítása	889
A nemautonóm többváltozós szabályozott szakaszok optimális irányítása	893
Kiegészítő megjegyzések	894
Néhány számpélda	895
Irodalom	898
Adaptív rendszerek	903
Az adaptív szabályozási rendszerek változatai	903
A passzív adaptáció	905
Adaptálódás a bemenőjelhez	906
Extremális rendszerek	907
Jel-adaptáció	907
Átviteli adaptáció	908
Kiegészítő megjegyzések	909
Néhány példa adaptív rendszerekre	910
Nagy hurokerősítő adaptív rendszerek	912
Előírt csillapítási tényzőjű adaptív rendszer	912
A rakétagyorsulás adaptív szabályozása	913
A bemenőjelhez adaptáló követőszabályozás	918
Modellre alapozott adaptív rendszerek	920
Irodalom	924
Optimumkereső rendszerek	924
Az optimumkereső rendszerek alapfogalmai	925
Az externális rendszerek néhány fajtája	926
A stacionárius folyamatok vizsgálata	940
Az optimumkeresés módszerei bonyolultabb rendszerekben	944
Az adaptáció, a tanulás, az optimumkeresés elméleti alapjai	950
Az optimalitás kritériumai	950
Az adaptáció folyamata és algoritmusa	951
Adaptáció korlátozások figyelembevételével	952
A tanuló alakfelismerés	953
Identifikáció	956
Adaptív szűrés	957
Adaptív (duális) irányítás	958
Irodalom	960
Függelék	965
A mátrixszámítás és a vektoranalízis néhány alaptétele	966
A mátrixalgebra néhány alaptétele	966
Bilineáris és kvadratikus alakok	970
Normák	971
A vektoranalízis alapjai	975
Néhány differenciálási szabály	979
Állapotváltozók, állapotegyenletek	983
A szabályozott szakasz átviteli mátrixának meghatározása az állapotegyenletekből	983
Az állapotegyenletek meghatározása az átviteli függvényből vagy az átviteli mátrixból	984
A visszacsatolt rendszerek állapotegyenletei	985
Normális szakaszok	990
A kanonikus alak	992
A fázisváltozós alak meghatározása	995
Irodalom	998
Az állapot-differenciálegyenletek megoldása	1000
Az állandó paraméterű lineáris homogén vektor-differenciálegyenlet megoldása	1000
Az alapmátrix meghatározása	1002
Az alapmátrix meghatározása többszörös sajátértékek fellépésekor	1007
Az állandó paraméterű inhomoégn állapotegyenlet megoldása	1008
Irodalom	1009
Változó együtthatójú differenciálegyenletek	1010
A változó paraméterű homogén állapotegyenlet megoldása	1010
Az inhomogén változó együtthatójú differenciálegyenlet megoldása	1012
A társrendszer	1014
Az átmeneti mátrix meghatározása	1016
Irodalom	1019
Az elérhetőség, az irányíthatóság, a megfigyelhetőség	1020
Az elérhető állapotok	1020
Az irányíthatóság és a megfigyelhetőség definícója	1020
A lineáris, állandó paraméterű rendszerek irányíthatósága	1021
A lineáris, állandó paraméterű rendszerek megfigyelhetősége	1024
Normális szakaszok	1026
Irodalom	1027
Mintavételező rendszerek állapot- és fázisegyenletei	1028
A homogén fázisegyenletek megállapítása	1028
A fázisváltozós alak meghatározása az impulzusátviteli függvényből	1031
A mintavételező rendszerek általános állapotegyenletei	1033
A lineáris állapotegyenletek megoldása	1036
A z-transzformáció	1038
Az átmeneti mátrix meghatározása	1040
A változó paraméterű szakasz átmeneti mátrixának meghatározása	1041
Az irányíthatóság, a megfigyelhetőség	1043
Az elméleti mechanika néhány összefüggése	1047
Alapfogalmak, alapösszefüggések	1047
A Lagrange-egyenlet	1051
Irodalom	1054
Idézett könyvek jegyzéke	1055
Tárgymutató	1075