1.062.439
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát
Kidolgozott példák lengéstanból
Kézirat/Budapesti Műszaki Egyetem Gépészmérnöki Kar
Budapest
| Kiadó: | Tankönyvkiadó Vállalat |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Ragasztott papírkötés |
| Oldalszám: | 244 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 24 cm x 17 cm |
| ISBN: | |
| Megjegyzés: | Kézirat. Tankönyvi szám: J4-370. Megjelent 287 példányban. 222 fekete-fehér ábrát tartalmaz. |
Értesítőt kérek a kiadóról
A beállítást mentettük,
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
A beállítást mentettük,
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Előszó
A gépészmérnök munkája sorén gyakran találkozik olyan mozgásokkal, amelyeket - az egyensúlyi helyzet körül - a rugalmas visszatérítő erő, csillapító erő és esetleg valamilyen gerjesztő hatás... TovábbElőszó
A gépészmérnök munkája sorén gyakran találkozik olyan mozgásokkal, amelyeket - az egyensúlyi helyzet körül - a rugalmas visszatérítő erő, csillapító erő és esetleg valamilyen gerjesztő hatás befolyásol. Ezekkel a mozgásokkal a kinetikának önálló ága, a lengéstan foglalkozik. Szerkezeteink nagy része kis rugalmasságú (merevnek tekinthető) tömegekből áll és ezeket rugalmas elemek (melyeknek tömege többnyire elhanyagolható) kapcsolják egymáshoz és más szerkezetekhez. Az egyes elemek rugalmas jellemzőinek meghatározására a szilárdságtan összefüggéseit használjuk fel, míg az erők vizsgálatában a statika tételeire támaszkodunk. A feladatok megoldása során többnyire mozgásegyenleteket írunk fel (álló vagy mozgó koordináta rendszerben), és a kinetikából még gyakran használjuk a súlypont- és munkatételt. VisszaTartalom
| Egytömegü, egyszabadságfoku lengőrendszerek | |
| Tömeg lengése vizszintes sima vezetékben | 5 |
| Rugóra függesztett test lengése | 7 |
| A lengőrendszer sajátkörfrekvenciájának meghatározásához eredő rugóállandót kell számitani | 12 |
| Az eredő rugóállandó a rugók kapcsolásának módjától függ | 15 |
| A rugótányérra helyezett test nagy kezdősebesség esetén elválik tőle | 16 |
| A helyettesitő rugó állandóját az energiák egyenlősége alapján is számithatjuk | 18 |
| Csapágyazott rud forgó lengése | 22 |
| Tengelyre ékelt tárcsa forgó lengése | 27 |
| Vizoszlop lengése | 33 |
| Szabad lengés Coulomb surlódással | 35 |
| A gumirugó csillapitja a lengést | 40 |
| Lengés haladó mozgást végző térben | 44 |
| Lengés forgó mozgást végző térben | 51 |
| A függesztő kötél tömegét egyszerüen Rayleigh módszerével vehetjük figyelembe | 56 |
| A surlódás következtében állandó sebességü vontatás esetén is rezgés tapasztalható | 62 |
| Nemlineáris szabad lengés | 72 |
| A rendszer egyik rugóját gerjesztő hatás éri | 77 |
| A gerjesztett lengést a rezonanciától távol a surlódás alig befolyásolja (egyenértékü csillapitás) | 82 |
| Gerjesztett, csillapitott lengés esetén a rugóerő és a kitérés általában nincs fázisban | 92 |
| A tömeg a rugón és a csillapitáson keresztül egyszerre is kaphat gerjesztést | 102 |
| A lengést forgattyus hajtómü gerjeszti, s igy a felharmonikusokra is gondolni kell (Fourier-sor) | 111 |
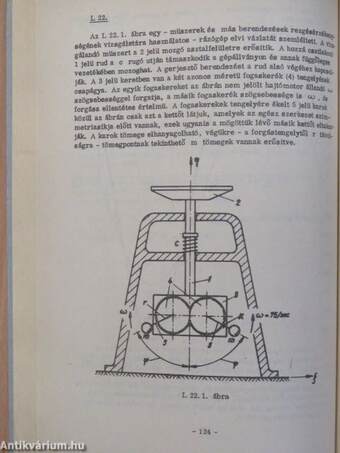
| Excentrikusan elhelyezett tömeg esetén a gerjesztő hatás a fordulatszám négyzetével arányos (rázóasztal) | 124 |
| A lengés méréséhez lengőrendszert használunk | 134 |
| Egytömegü, kétszabadságfoku lengőrendszerek | |
| A tömegpont általános mozgása Lissajous görbe (Befogott függőleges rud végén tömegpont) | 146 |
| Állandó irányu harmonikus gerjesztés esetén a tömegpont egyenes pályán mozog (Nyitott keret végén tömegpont) | 158 |
| A függőleges rugókra helyezett merev rud is kétszabadságfoku lengőrendszernek tekinthető | 168 |
| Láncszerüen elhelyezett többtömegü lengőrendszerek | |
| A karakterisztikus egyenlet a mozgásegyenletek alapján kapható | 178 |
| Bonyolultabb rendszer tömegredukálással egyszerüsithető | 187 |
| A kötött rendszer vizsgálatát szabad rendszer vizsgálatára vezetjük vissza. Közelitések | 189 |
| A sajátkörfrekvenciák meghatározására szerkesztő módszerek is alkalmazhatók | 199 |
| Az inditástól függő általános mozgás a sajátlengések szuperpoziciója | 206 |
| A lengéskép ismerete megkönnyiti a vizsgálatainkat. (Gerjesztett lengés) | 213 |
| Hajlitó lengés és kritikus fordulatszám | |
| A hajlitott tartó rugóállandója is a rugóállandó definiciója alapján határozható meg | 221 |
| A két tömeg a kisebb sajátfrekvencia esetén fázisban, nagyobbnál ellenfázisban leng | 225 |
| A Ryleigh módszer a pontos értéknél nagyobb sajátfrekvenciát ad (Laprugó) | 230 |
| A kritikus fordulatszám közelében nem üzemeltethető a forgó tengely | 236 |
| A kritikus szögsebesség nagysága megegyezik a lengőrendszer sajátkörfrekvenciájával | 238 |
| Három tárcsa esetén Dunkerley módszerét használhatjuk | 239 |
Témakörök
- Műszaki > Gépészet
- Műszaki > Géptan, gépészet > Gépelemek > Egyéb
- Természettudomány > Fizika > Feladatok > Példatár
- Természettudomány > Fizika > Mechanika
- Természettudomány > Fizika > Tankönyvek > Felsőoktatási
- Természettudomány > Fizika > Társtudományok > Műszaki
- Műszaki > Géptan, gépészet
- Műszaki > Tankönyvek, jegyzetek, szöveggyűjtemények > Felsőoktatási
- Tankönyvek, jegyzetek, szöveggyűjtemények > Természettudományok > Fizika > Felsőoktatási
- Tankönyvek, jegyzetek, szöveggyűjtemények > Műszaki > Felsőoktatási > Gépészet, géptan
Szücs Miklós
Szücs Miklós műveinek az Antikvarium.hu-n kapható vagy előjegyezhető listáját itt tekintheti meg: Szücs Miklós könyvek, művekMegvásárolható példányok
Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.
Folytatás Microsoft-tal