1.117.306
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát
Felsőbb matematikai összefoglaló műszakiaknak
| Kiadó: | Műszaki Könyvkiadó |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Könyvkötői papírkötés |
| Oldalszám: | 644 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 18 cm x 12 cm |
| ISBN: | |
| Megjegyzés: | 201 fekete-fehér ábrával illusztrálva. Tankönyvi szám: 70121. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Tartalom
I. fejezet Egy- és többváltozós függvényekA) Alapfogalmak 11
1. Halmazok - 2. Struktúrák - 3. Valós számok - 4. Komplex számok - 5. Koordinátarendszerek - 6. Derékszögű koordinátarendszerek közötti koordinátatranszformációk
B) Az egyváltozós függvény 33
1. Az egyváltozós függvény fogalma - 2. Az egyváltozós függvény néhány fontos speciális tulajdonsága - 3. Az egyváltozós függvény határértéke és folytonossága
C) Alapfüggvények, nevezetes görbék 44
1. Szakaszonként egyenesvonalú függvények - 2. Algebrai függvények - 3. Elemi transzcendens függvények - 4. Nevezetes síkgörbék paraméteres egyenletei - 5. Nevezetes síkgörbék polárkoordinátás egyenletei - 6. Másodrendű görbék
D) A többváltozós függvény 80
1. A két- és többváltozós függvény fogalma - 2. A két- és többváltozós függvény határértéke és folytonossága
E) Felületek, felületi görbék 84
1. A felületek megadása - 2. Nevezetesebb felületek - 3. Másodrendű felületek - 4. Felületi görbék
II. fejezet Differenciálszámítás
A) Egyváltozós függvények deriválása 113
1. A differenciálhányados fogalma - 2. Differenciálási (deriválási) szabályok - 3. Nevezetesebb függvények deriváltjai - 4. Jobb- és baloldali differenciálhányados - 5. Végtelen differenciálhányados - 6. Magasabbrendű differenciálhányadosok - 7. A differenciál
B) A differenciálszámítás alaptételei 130
1. Rolle tétele - 2. Lagrange-féle középértéktétel - 3. Cauchy-féle középértéktétel - 4. Darboux tétele - 5. L'Hospital-szabály
C) Egyváltozós függvények vizsgálta 135
1. Monoton függvények - 2. Két függvény összehasonlítása - 3. Konvexitás, konkávitás és inflexiós pont - 4. Szélsőértékek
D) Ívelem, érintő, normális 140
1. Ívelem - 2. Tangens, normális, szubtangens és szubnormális (érintési paraméterek)
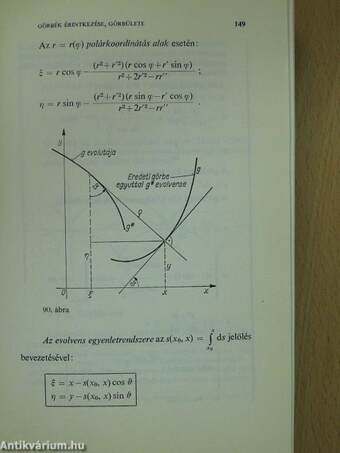
E) Görbék érintkezése és görbülete 144
1. Görbék érintkezése - 2. Simulókör (görbületi kör), görbület - 3. Evoluta, evolvens
F) A Taylor-sor 151
G) Többváltozós függvények deriválása 156
1. Parciális differenciálhányados - 2. Magasabbrendű parciális differenciálhányadosok - 3. A függvény teljes megváltozása és a teljes differenciál - 4. Összetett és implicit függvény deriválása - 5. Paraméteres alakban adott függvények deriválása - 6. Az iránymenti derivált és a gradiens
H) Kétváltozós függvény Taylor-formulája és Taylor-sora 173
I) Többváltozós függvények szélsőértéke 176
1. Felületi pontok osztályozása - 2. Szélsőérték létezésének szükséges és elégséges feltétele - 3. Feltételes szélsőérték - 4. Alkalmazás a kiegyenlítő számításban
III. fejezet Integrálszámítás
A) A határozatlan integrál 187
1. A határozatlan integrál fogalma, integrálási szabályok - 2. Integrálási módszerek - 3. Néhány függvénytípus integrálása
B) A határozott integrál 202
1. A határozott integrál fogalma, tulajdonságai - 2. Az integrálszámítás középértéktételei, az integrál mint felső (alsó) határának függvénye - 3. Paraméteres integrál
C) A határozott integrál alkalmazásai 217
1. Területszámítás - 2. Ívhossz-számítás - 3. Forgástest térfogatának kiszámítása - 4. Forgástest felszínének kiszámítása - 5. Mechanikai alkalmazások
D) Impropius integrálok 247
E) A határozott integrál közelítő kiszámítása 255
1. A határozott integrál becslése - 2. Numerikus integrálás - 3. Grafikus integrálás
F) Kettős és kétszeres integrál 265
1. A kettős integrál fogalma - 2. A kettős integrál kiszámítása, a kétszeres integrál
G) A kettős integrál alkalmazásai
1. Területszámítás - 2. Térfogatszámítás - 3. Felszínszámítás - 4. Mechanikai alkalmazások
H) A hármas integrál és alkalmazásai 292
1. A hármas integrál és kiszámítása - 2. A hármas integrál alkalmazásai
I) Vonalintegrál, felületi integrál, térfogati integrál 305
1. Vonalintegrál - 2. Felületi integrál - 3. Térfogati integrál
IV. fejezet Végtelen sorozatok, sorok és szorzatok
A) Számsorozatok 319
1. A sorozat fogalma és tulajdonságai - 2. A sorozat határértéke
B) Függvénysorozatok 329
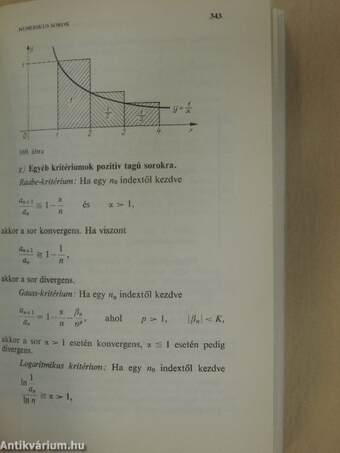
C) Numerikus sorok 333
1. A végtelen sor értelmezése, konvergenciája - 2. Konvergenciakritériumok - 3. Abszolút és feltételes konvergencia - 4. Műveletek sorokkal
D) Függvénysorok 350
E) Hatványsorok 354
1. A hatványsor értelmezése és konvergenciája - 2. Hatványsorok további tulajdonságai - 3. Függvények sorbafejtése
F) Sorok összegének számítása, hibabecslés 371
1. Sorok összegének számítása - 2. Hibabecslés
G) Fourier-sorok 384
H) Végtelen szorzatok 390
1. Numerikus (állandó elemű) szorzatok - 2. Függvényszorzatok
V. fejezet Lineáris algebra, vektoranalízis
A) Vektoralgebra 397
1. A vektor fogalma, műveletek értelmezése - 2. A műveletek elvégzése derékszögű koordinátákkal - 3. Reciprok vektorhármas - 4. Vektorok lineáris függősége
B) Mátrixalgebra, determinánsok, lineáris egyenletrendszerek 402
1. Mátrixalgebra - 2. Determinánsok - 3. Lineáris egyenletrendszerek
C) Tenzoralgebra 423
1. Értelmezés - 2. Műveletek tenzorokkal - 3. A tenzorok tulajdonságai, alkalmazások
D) Térgörbék 432
1. A vektor-skalár-függvény - 2. Térgörbék vizsgálata - 3. Felületi görbék differenciálgeometriája
E) A skalár-vektor-függvény 449
1. Értelmezés, ábrázolás - 2. Differenciálás, a gradiensvektor - 3. Integrálás
F) A vektor-vektor-függvény 458
1. Értelmezés, ábrázolás - 2. Differenciálás - 3. Műveletek a nablavektorral - 4. Integrálás
G) Integrálátalakítási tételek, a gradiens, divergencia és rotáció koordinátamentes értelmezése 474
1. A Gauss-Osztrogradszkij-tétel - 2. A Stokes-tétel - 3. Green-tételek - 4. A gradiens, divergencia és rotáció koordinátamentes értelmezése
H) A potenciálfüggvény 484
VI. fejezet Közönséges differenciálegyenletek
A) A differenciálegyenlet fogalma, osztályozása, megoldása 491
B) Elsőrendű differenciálegyenletek 494
1. Az y'=F(x,y) megoldhatósága - 2. Iránymező - 3. Görbesereg differenciálegyenlete
C) Bizonyos típusú elsőrendű differenciálegyenletek megoldása 501
1. Szétválasztható változójú differenciálegyenlet - 2. Szétválasztható változójúra visszavezethető differenciálegyenletek - 3. Az elsőrendű lineáris differenciálegyenlet - 4. A Bernoulli-féle differenciálegyenlet - 5. A Riccati-féle differenciálegyenlet - 6. Egzakt differenciálegyenlet - 7. Az elsőrendű differenciálegyenlet szinguláris megoldása - 8. Lagrange- és Clairaut-féle differenciálegyenlet - 9. Ortogonális és izogonális trajektóriák
D) Egyes magasabbrendű differenciálegyenletek megoldása 546
1. A változó együtthatójú n-edrendű lineáris differenciálegyenlet - 2. Állandó együtthatójú n-edrendű lineáris differenciálegyenlet - 3. Az n-edrendű Euler-féle differenciálegyenlet - 4. Néhány speciális másodrendű differenciálegyenlet megoldása
E) Differenciálegyenlete megoldása végtelen sorok segítségével 581
F) Közönséges differenciálegyenlet-rendszerek 591
1. Megoldhatóság és visszavezetés differenciálegyenletre - 2. Lineáris differenciálegyenlet-rendszer
VII. fejezet Parciális differenciálegyenletek
A) A parciális differenciálegyenlet fogalma és osztályozása 609
B) Az elsőrendű lineáris parciális differenciálegyenlet 612
C) Az általános elsőrendű parciális differenciálegyenlet 614
1. Karakterisztikus görbe, karakterisztikus sáv - 2. Cauchy-feladat
D) Néhány nevezetes magasabbrendű parciális differenciálegyenlet 621
1. A hővezetés (és diffúzió) differenciálegyenlete - 2. A rezgő húr és a rezgő membrán differenciálegyenlete (D'Alembert-féle differenciálegyenlet) - 3. A Laplace- és a Poisson-egyenlet - 4. A biharmonikus egyenlet
Irodalom 643
Témakörök
- Természettudomány > Matematika > Algebra és számelmélet > Általában
- Természettudomány > Matematika > Analízis > Általában
- Természettudomány > Matematika > Tankönyvek > Felsőfokú
- Természettudomány > Matematika > Társtudományok > Műszaki
- Tankönyvek, jegyzetek, szöveggyűjtemények > Természettudományok > Matematika > Felsőfokú
Megvásárolható példányok
Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.