1.116.716
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát
Analízis
Kézirat
| Kiadó: | Tankönyvkiadó Vállalat |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Ragasztott papírkötés |
| Oldalszám: | 252 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 24 cm x 17 cm |
| ISBN: | |
| Megjegyzés: | Kézirat. A könyv tankönyvi száma: J010-1023. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Tartalom
| Előszó | 3 |
| Halmazok, leképezések, függvények | 5 |
| Halmazok, halmazok számossága | 5 |
| Függvények, operációk | 15 |
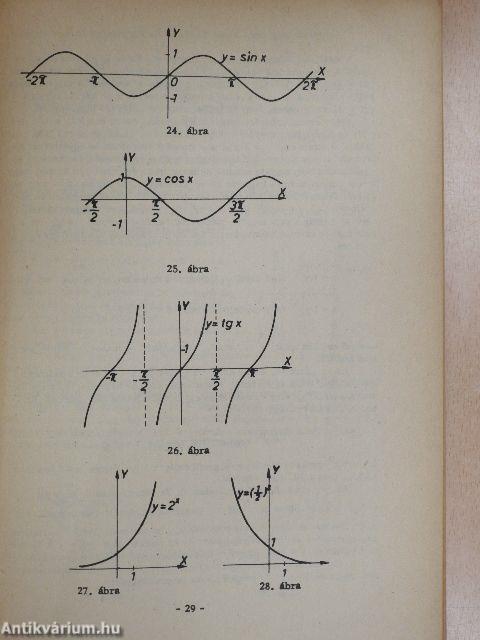
| Függvények grafikonja, alapfüggvények | 25 |
| Paraméteres alakban megadott függvények | 34 |
| A határérték | 36 |
| Környezet. Torlódási hely. Számsorozat | 36 |
| Összehúzódó zárt intervallumok elve | 40 |
| A határérték fogalma | 44 |
| A határérték-tulajdonságok | 45 |
| Példák sorozatokra | 49 |
| Folytonos és szakadásos függvények | 57 |
| Függvények határértéke | 57 |
| Példák folytonos függvényekre | 61 |
| A gyakorlatban előforduló néhány fontosabb függvény | 64 |
| Folytonos függvények alaptulajdonságai | 68 |
| Differenciálhányados, derivált függvény, deriválási szabályok, elaszticitás | 70 |
| A differnciálhányados fogalma | 70 |
| A különbségi hányados és differenciálhányados geometriai és mechanikai jelentése | 72 |
| A derivált függvény | 74 |
| Az alapfüggvények derivált függvénye | 74 |
| Magasabbrendű deriváltak | 82 |
| A függvény elaszticitása | 83 |
| A differenciálszámítás alaptételei, függvények vizsgálata | 86 |
| Függvények növekedése és csökkenése | 86 |
| Helyi szélső értékek | 88 |
| Konvex és konkáv függvények, inflexiós pont | 95 |
| Taylor sor, egyenletek valós gyökei | 102 |
| Taylor-polinom, Taylor-sor maradéktagja, maclaurin-sor | 102 |
| Taylor-sor felhasználása, helyi szélső értékek meghatározása | 110 |
| A Taylor-polinom algebrai vontakozásai | 113 |
| Egyenletek valós gyökeinek közelítő meghatározása | 116 |
| Végtelen sorok | 119 |
| A függvényvizsgálat alkalmazásai | 129 |
| Maximum-minimum feladatok | 129 |
| Költségfüggvény | 145 |
| Megjegyzések a maximum-minimum számításához | 150 |
| Határozott és határozatlan integrál | 152 |
| A határozott integrál fogalma | 152 |
| Határozott integrál fontosabb tulajdonságai | 157 |
| A határozatlan integrál | 159 |
| A Leibnitz-Newton-féle képlet | 163 |
| A parciális integrálás módszere | 166 |
| Integrálás helyettesítéssel | 168 |
| Az integrálszámítás néhány alkalmazása | 172 |
| A határozott integrál és primitív függvény közelítő kiszámítása | 184 |
| Improprius integrálok | 189 |
| Többváltozós függvények | 194 |
| A többváltozós függvény fogalma | 194 |
| Többváltozós függvény határértéke, folytonossága | 202 |
| A parciális differenciálhányados | 203 |
| Magasabbrendű parciális deriváltak | 206 |
| Szélsőértékek | 208 |
| Feltételes szélsőérték | 215 |
| A Lagrange-féle multiplikátor módszer | 219 |
| Differenciálegyenletek | 226 |
| Közönséges differenciálegyenlet fogalma | 226 |
| Változók szétválasztásával megoldható differenciálegyenlet | 227 |
| Homogén differenciálegyenlet | 231 |
| Homogén visszavezethető differenciálegyenletek | 234 |
| Lineráris differenciálegyenletek | 236 |
| Elsőrendű lineáris differenciálegyenletek | 237 |
| Homogén lineáris differenciálegyenlet állandó együtthatókkal | 240 |
| Inhomogén lineáris differenciálegyenlet | 245 |
| Kezdeti feltételek | 249 |
| Differenciálegyenletek megoldásának egyik numerikus módszere | 249 |