1.068.961
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát

VISSZA
A TETEJÉRE
JAVASLATOKÉszre-
vételek
Matematika-2
Analízis
| Kiadó: | SZÁMALK Kiadó |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Ragasztott papírkötés |
| Oldalszám: | 261 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 24 cm x 17 cm |
| ISBN: | |
| Megjegyzés: | Fekete-fehér ábrákkal. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Tartalom
| A függvény | 1 |
| A függvény matematikai fogalma | 1 |
| A függvény ábrázolása | 3 |
| Descartes-féle koordináták | 3 |
| Polárkoordináták | 6 |
| A függvények osztályozása | 10 |
| A fügvénnyel kapcsolatos alapfogalmak | 12 |
| Korlátosság | 12 |
| Szélsőértékhely | 13 |
| Monotonitás | 14 |
| Tükrözési szimmetriák | 15 |
| Periodicitás | 16 |
| Az inverz függvény | 16 |
| Az első fejezet összefoglalása | 18 |
| Feladatok | 19 |
| A függvény határértéke, folytonossága | 21 |
| A véges határérték | 21 |
| A véges határérték | 21 |
| A végtelen, mint határérték | 24 |
| Néhány elemi függvény határértéke | 24 |
| Egy fontos speciális eset | 25 |
| Összeg, szorzat és hányados határértéke | 26 |
| Bal és kobb oldali határérték | 27 |
| Határérték a végtelenben | 28 |
| A határérték Cauchy-féle definíciója | 30 |
| Függvény folytonossága | 30 |
| A folytonosság fogalma | 31 |
| Folytonos függvények egy fontos tulajdonsága | 32 |
| Az érintő | 34 |
| A második fejezet összefoglalása | 36 |
| Feladatok | 38 |
| Valós egyváltozós függvények | 39 |
| Elemi függvények | 39 |
| Lineáris függvény | 39 |
| Reciprok függvény | 40 |
| Hatványfüggvény és irracionális függvény | 41 |
| Exponenciális függvény és logaritmusfüggvény | 43 |
| Trigonometrikus függvények, szinusz, koszinusz és inverzeik | 45 |
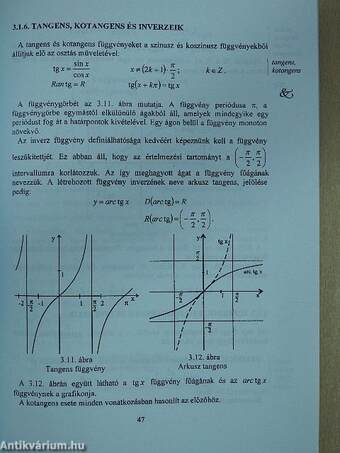
| Tangens, kotangens és inverzeik | 47 |
| Hiperbolikus függvények és inverzeik | 48 |
| Fontosabb leszármazott függvények | 53 |
| A leszármaztatás módjai | 53 |
| Racionális egész függvények | 54 |
| Racionális törtfüggvények | 56 |
| Haranggörbe | 59 |
| Szakaszonként lineáris függvények | 59 |
| Függvények paraméterezése | 61 |
| Paraméteres egyenletek | 63 |
| A harmadik fejezet összefoglalása | 65 |
| Differenciálszámítás | 67 |
| A differenciálhányados (derivált) | 68 |
| A differenciahányados | 68 |
| A differenciálhányados | 69 |
| A differenciálhatóság | 71 |
| A differenciálhányados geometriai jelentése | 73 |
| Néhány elemi függvény deriváltfüggvénye | 74 |
| Differenciálási szabályok | 76 |
| Függvények összegének, különbségének, szorzatának, hányadosának, konstansszorosának deriváltja | 77 |
| Összetett függvény deriváltfüggvénye. Implicit függvények | 80 |
| Függvény inverzének a deriváltja | 84 |
| További elemi függvények deriváltjai | 85 |
| A differenciál | 90 |
| Magasabbrendű deriváltak | 92 |
| A differenciálszámítás középértéktételei | 93 |
| A negyedik fejezet összefoglalása | 95 |
| Feladatok | 97 |
| A differenciálszámítás néhány alkalmazása | 101 |
| Maclaurin- és Taylor-polinom | 101 |
| A Maclaurin-polinom | 101 |
| A Taylor-polinom | 103 |
| A L'Hospital-szabály | 107 |
| Az ötödik fejezet összefoglalása | 115 |
| Feladatok | 116 |
| Függvények diszkussziója a deriváltak segítségével | 119 |
| Monoton függvények | 119 |
| A szélsőérték meghatározása | 121 |
| A szükséges feltétel | 121 |
| Az elégséges feltétel | 122 |
| Konvexség, konkávság, inflexiós pont | 126 |
| A hatodik fejezet összefoglalása | 131 |
| Feladatok | 133 |
| Határozatlan integrál | 135 |
| Bevezetés | 135 |
| Primitív függvény, határozatlan integrál | 136 |
| Alapintegrálok | 137 |
| Integrálási szabályok | 138 |
| Parciális integrálás | 140 |
| Integrálás helyettesítéssel | 143 |
| Racionális törtfüggvény integrálás | 146 |
| A határozatlan integrál néhány sajátsága | 150 |
| A hetedik fejezet összefoglalása | 151 |
| Feladatok | 154 |
| Határozott integrál | 159 |
| Bevezetés | 159 |
| A határozott integrál fogalma | 161 |
| A határozott integrál tulajdonságai | 165 |
| A Newton-Leibniz-formula | 168 |
| Középérték-tétel és integrálfüggvény | 170 |
| Improprius integrálok | 172 |
| A nyolcadik fejezet összefoglalása | 175 |
| Feladatok | 177 |
| A határozott integrál néhány alkalmazása | 179 |
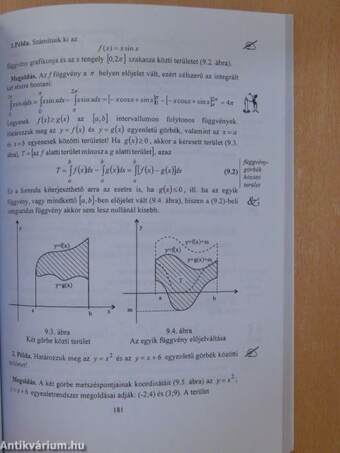
| Területszámítás | 179 |
| A szektor területe | 183 |
| Ívhosszúság kiszámítása | 187 |
| Testek térfogata, forgástest térfogata és felszíne | 191 |
| A kilencedik fejezet összefoglalása | 197 |
| Feladatok | 200 |
| Függvénysorozatok és függvénysorok | 201 |
| A függvénysorozat fogalma | 201 |
| Az egyenletes konvergencia | 203 |
| A függvénysor fogalma | 206 |
| Hatványsorok | 209 |
| A Taylor-sor | 209 |
| Nevezetes (Maclaurin) hatványsorok | 217 |
| Fourier-sorok | 219 |
| A tizedik fejezet összefoglalása | 221 |
| Feladatok | 223 |
| Többváltozós függvények | 227 |
| Kétváltozós függvények | 227 |
| A kétváltozós függvény értelmezése | 227 |
| A kétváltozós függvény ábrázolása | 229 |
| Felületek egyenletének felírása, nevezetes felületek | 232 |
| A kétváltozós függvény határértéke és folytonossága | 234 |
| A parciális derivált | 235 |
| Többszörös parciális derivált | 237 |
| Differenciálási szabályok | 238 |
| Az iránymenti derivált | 239 |
| A teljes differenciál | 240 |
| Felület érintősíkja | 242 |
| A többváltozós függvény | 243 |
| Kétváltozós függvény szélsőértéke | 249 |
| Feltételes szélsőérték | 249 |
| Kétváltozós függvény integrálja | 251 |
| A térfogat mint kettős integrál | 253 |
| A kettős integrál kiszámításának módja | 253 |
| A tizenegyedik fejezet összefoglalása | 255 |
| Feladatok | 258 |