1.067.081
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát

VISSZA
A TETEJÉRE
JAVASLATOKÉszre-
vételek
Ábrázoló geometria
Egyetemi tankönyv
| Kiadó: | Tankönyvkiadó Vállalat |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Fűzött keménykötés |
| Oldalszám: | 413 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 24 cm x 17 cm |
| ISBN: | |
| Megjegyzés: | 556 fekete-fehér ábrával, Anaglif ábrák című melléklettel (tűzött kötésben) illusztrálva. Tankönyvi szám: 44 333. 3D szemüveggel. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Fülszöveg
A tankönyv a Nehézipari Műszaki Egyetem ábrázoló geometriai programjában körvonalazott tananyagot tárgyalja. A korlátozott terjedelem és az oktatási cél szem előtt tartásával mellőznünk kell a geometria axiomatikus tárgyalását. Éppen ezért - a műszaki egyetemek gyakorlata szerint - kénytelenek vagyunk sokkal többet a szemléletre támaszkodva elfogadni, mint amennyit matematikailag kifogástalan feldolgozás esetén megengedhetünk magunknak. A szemléletességet szolgálja a tankönyv bőséges ábraanyaga és a melléklet anaglif ábrái. Igyekszünk a szemléletesebb utat választani, ha az nem megy a szabatosság rovására. A „közvetlenül belátható" bizonyításával- ahol az veszéllyel nem jár - azért sem foglalkozunk, hogy több időnk maradjon a legfőbb cél, a konstruktív geometriai érzék, a praktikus térszemlélet és a szerkesztőmunka készségének kifejlesztésére. Azok számára, akik ismeretük minden részletét szilárd alapra kívánják helyezni, megfelelő irodalmat ajánlunk. A tananyag feldolgozása... TovábbFülszöveg
A tankönyv a Nehézipari Műszaki Egyetem ábrázoló geometriai programjában körvonalazott tananyagot tárgyalja. A korlátozott terjedelem és az oktatási cél szem előtt tartásával mellőznünk kell a geometria axiomatikus tárgyalását. Éppen ezért - a műszaki egyetemek gyakorlata szerint - kénytelenek vagyunk sokkal többet a szemléletre támaszkodva elfogadni, mint amennyit matematikailag kifogástalan feldolgozás esetén megengedhetünk magunknak. A szemléletességet szolgálja a tankönyv bőséges ábraanyaga és a melléklet anaglif ábrái. Igyekszünk a szemléletesebb utat választani, ha az nem megy a szabatosság rovására. A „közvetlenül belátható" bizonyításával- ahol az veszéllyel nem jár - azért sem foglalkozunk, hogy több időnk maradjon a legfőbb cél, a konstruktív geometriai érzék, a praktikus térszemlélet és a szerkesztőmunka készségének kifejlesztésére. Azok számára, akik ismeretük minden részletét szilárd alapra kívánják helyezni, megfelelő irodalmat ajánlunk. A tananyag feldolgozása ábrázoló geometriai előtanulmányokat nem tételez fel.Mind a tananyag kiválasztása, mind a tárgyalás módszere alkalmazkodik a rokon tantárgyak és különösen a konstrukciós szaktárgyak igényeihez, és számukra alapos geometriai, ábrázolási és szerkesztési ismereteket ad. A tankönyv tömörségre törekszik. Mégis a lényeges ismeretek összefüggéseikkel - különféle megvilágításban - kerülnek tárgyalásra.
A szemléltető ábrák, valamint az anaglif ábrák a térbeli mintákat helyettesítik. Amikor már az alapozásnál is a szemléltető ábrák számát a szerkesztési ábrák-hoz viszonyítva a legszükségesebbre szorítjuk le, ezzel az a célunk, hogy a kezdőt minél előbb mintegy „kényszerítsük" a legjelentősebb készség kifejlesztésére: merőleges vetületekből a térbeli alakzat önálló elképzelésére.
Rendszerbe foglaljuk azokat az alapvető ismereteket, amelyekre a gyakorlati alkalmazás számít. Átfogó elvek kiemelésével széleskörű önálló alkalmazási képesség kifejlesztésére törekszünk. A tananyag minden részletében az elmélet és a gyakorlat szoros egysége jut kifejezésre. Elsősorban az a célunk, hogy az anyag elsajátításával az olvasó megfelelő találékonyságra tegyen szert ahhoz, hogy gyakorlati feladatok geometriai tartalmát felismerje, sikeresen birkózzon meg egy-egy kérdés szabatos geometriai megfogalmazásával. Vissza
Tartalom
ELSŐ RÉSZALAPVETŐ GEOMETRIAI ÉS ÁBRÁZOLÁSI ISMERETEK
I. Bevezetés..............................13
1. Az ábrázoló geometriáról .......................................................13
2. Történeti áttekintés......................................14
II. Geometriai alapvetés .....................................................15
3. A geometriáról ..........................................................15
4. Párhuzamosság ............................................................16
5. Térelemek.......................................................................................17
6. Térelemek kölcsönös helyzete..............................................18
7. Térelemek meghatározása.........................................................19
8. Térelemekre vonatkozó tételek....................................20
9. Alapalakzatok és alaprendszerek..............................................25
10. Sík- és térmértani szerkesztések....................................................27
III. Ábrázolás ..................................................................29
11. Az ábrázolásról általában .............................................29
12. Vetítés és vetítési módszerek...........................29
13. Egyértelmű ábrázolási rendszerek ...........................31
14. Szakasz, síkidom és szög vetülete .................................34
ÁBRÁZOLÁS RENDEZETT MERŐLEGES VETÜLETEKBEN
IV. Térelemek ábrázolása ..................................................................37
15. A képsíkrendszer.....................................37
16. A pont ábrázolása .........................................38
17. Fedőpontok...............................................................41
18. Alakzat ábrázolása ......................................................................41
19. A harmadik képsík.....................................................................43
20. Képsíkváltás (transzformáció) ...............................................44
21. Alakzat új képe.........................................................................................46
22. A képtengely elhagyása .....................................................48
23. Szakasz rendezett képei.......................................49
24. Az egyenes ábrázolása............................................................50
25. Az egyenes új képe ...................................................53
26. Két egyenes kölcsönös helyzete ......................................54
27. A sík ábrázolása..........................................55
28. Végtelen távoli térelemek ábrázolása.....................................59
V. Térelemek helyzetgeometriája .................................................................59
29. Illeszkedések ................................................................60
30. Összekötések ................................................................61
31. A sík különleges egyenesei ..................................63
32. Síkidom ábrázolása .................................................................64
33. Két sík metszésvonala .............................................65
34. Sík és egyenes döféspontja ....................................................68
35. Két síkidom metszése.............................................71
36. Transzverzálisok.................................................................................72
37. Alkalmazás: árnyékszerkesztés........................................74
VI. Térelemek méretgeometriája ...................................................78
38. Célszerű új nézetek szerkesztése...............................................78
39. A forgatás .......................................................80
40. Elforgatás.................................................................81
41. Sík leforgatása képsíkba ........................................82
42. Affinitás............................................................85
43. Sík leforgatása főállásba............................................................87
44. Sík visszaállítása...........................................................88
45. Egymásra merőleges térelemek ábrázolása...............................................90
46. Két pont távolsága.........................................................92
47. Pont és sík távolsága ......................................................93
48. Sík és vele párhuzamos egyenes távolsága...................................................94
49. Két párhuzamos sík távolsága .......................................................95
50. Pont és egyenes távolsága..................................................................95
51. Két párhuzamos egyenes távolsága ......................................96
52. Két kitérő egyenes távolsága..................................................................97
53. Két egyenes szöge.............................................99
54. Sík és egyenes szöge.............................................................100
55. Két sík szöge........................................................101
56. Két sík szögfelező síkjai .............................................................102
57. Megoldandó feladatok....................................................103
VII. Síklapú alakzatok ................................................104
58. Síklapú testekről általában ..........................................105
59. Paralelogramma alapú hasáb ...............................................................106
60. Gúla- és hasábfelületek .......................................... 107
61. Hasáb ábrázolása és síkmetszése ............................................108
62. Gúla ábrázolása és síkmetszése ........................................................112
63. Centrális kollineáció.........................................................114
64. Gúla, illetve hasáb döfése egyenessel ...........................................117
65. Gúla és hasáb áthatása ................................................................119
66. Szabályos testek ...................................................................126
67. Szabályos tetraéder......................................................129
68. Szabályos oktaéder .........................................................130
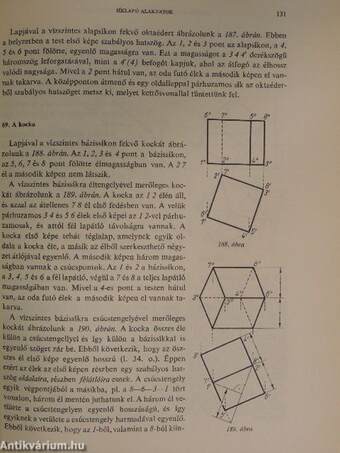
69. A kocka .........................................................................131
70. Síklapú alakzatok határlapjainak síkba terítése.............................133
VIII. Mértani feltételnek megfelelő térelemek ....................................136
71. A geometriai feltételek kiszabása..........................................137
72. Térelemtől adott távolságra levő térelemek ......................................138
73. Térelemmel adott szöget bezáró térelemek...............................143
74. Térelemekhez adott méretre levő térelemek..............................146
75. Térelemektől egyenlő méretre levő térelemek......................................150
76. Feladatok térelemek meghatározására ..........................................152
77. Megoldandó feladatok......................................................154
ÁBRÁZOLÁS KÉPIES VETÜLETEKBEN
IX. Axonometria............................................................ 156
78. Az axonometrikus ábrázolás............................................. 156
79. Helyzetfeladatok axonometriában ........................................ 157
X. Különféle axonometriák................................................... 163
80. Merőleges axonometria ................................................. 163
81. Méretfeladatok merőleges axonometriában ................................. 166
82. A ferde axonometria válfajai ............................................ 169
83. Méretfeladatok kavalier-axonornetriában.................................. 171
84. Ábrázolás általános axonometriában...................................... 173
XI. Centrális vetület, perspektíva.............................................. 174
85. Centrális vetítés........................................................ 175
86. Alakzat perspektívája.................................................. 177
MÁSODIK RÉSZ
GÖRBE VONALAK ÉS EGYSZERŰ FELÜLETEK
XII. Síkgörbék.............................................................. 181
87. A görbe vonalakról általában........................................181
88. A síkgörbék különleges pontjai és érintői................................183
89. Tapasztalati görbék megrajzolása ..................................................185
90. A kör és vetületei ..........................................................187
91. A kör és ellipszis affin vonatkozása...................................189
92. Tengelyszerkesztés társátmérőpárból.......................................192
93. Ellipszist rajzoló eszközök.............................................................193
94. Másodrendű görbék származtatása, a kúpszeletek .........................................194
95. Az ellipszis származtatása és szerkesztése............................................195
96. A hiperbola származtatása és szerkesztése ....................................200
97. A parabola származtatása és szerkesztése............................202
98. Néhány különleges kúpszelet szerkesztés............................205
99. Kúpszeletek simulókörei .....................................................206
100. A kosárgörbe..................................................................210
101. A kör ábrázolása ................................................211
102. Ellipszis, hiperbola és parabola ábrázolása ..........................214
XIII. A gömb...........................................................................................215
103. A felületekről általában...........................................................216
104. A gömb ábrázolása............................................219
105. Gömbfelületi pont, érintő, érintősík, normális..................................222
106. Gömb metszése síkkal és egyenessel ...............................................223
107. Gömbök áthatása.........................................225
XIV. Kúp- és hengerfelületek...................................226
108. A kúp- és hengerfelületekről általában ......................................226
109. A forgáshenger ábrázolása ............................................228
110. Forgáshenger metszése egyenessel és síkkal, síkba terítése ................229
111. A ferde körhenger ábrázolása, síkmetszése, síkba terítése...................232
112. A forgáskúp ábrázolása........................................234
113. Forgáskúp metszése egyenessel és síkkal, síkba terítése................236
114. A ferde körkúp ábrázolása, síkmetszése, síkba terítése ....................242
XV. Kúp, henger és gömb áthatása......................................245
115. A térgörbe vetülete...........................................245
116. Áthatással keletkező negyedrendű térgörbe ................................247
117. Egyszerű áthatások, kettős vetületek..................................248
118. Két másodrendű görbére széteső áthatás ...........................253
119. Sztereografikus vetület.......................................................256
120. Forgáshenger és forgáskúp áthatása axonometriában .................256
121. A negyedrendű térgörbe különleges pontjai...............................260
122. Két részből álló áthatási görbe..................................261
123. Kettős-, csúcs- és remetepont az áthatási görbén.......................262
124. Végtelen távoli pont a görbén és további szétesések..........................264
XVI. Forgásfelületek ................................................................265
125. A forgásfelületről általában.............................................265
126. Másodrendű forgásfelületek ......................................................266
127. A forgáskörgyűrű ábrázolása, síkmetszése.........................269
128. Forgásfelületek áthatása ......................................................273
129. Forgásfelület képhatára.......................................276
A MOZGÁSGEOMETRIA ALAPJAI
XVII. Mozgással származó síkgörbék.............................................281
130. A merev sík mozgása.................................................. 281
131. Gördülő mozgás..............................................................283
132. Ruletták.................................................284
133. Homlokkerekek fogprofilja.................................287
XVIII. Mozgással származó térgörbék .........................................290
134. Evolvens fogazású kúpkerekek.................................291
135. Alkotó mentén érintkező hiperboloidok..........................................292
136. A csavarvonal származása, kiteríthető felülete.........................294
137. A csavarvonal különféle vetületei.....................................298
138. Csavarmozgással fedésbe hozott háromszögek .............................299
A MŰSZAKI GYAKORLATBAN ALKALMAZOTT TOVÁBBI FELÜLETEK
XIX. Csavarfelületek és más különleges felületek ......................302
139. Egyenes vonalú csavarfelületek, csavarok...................................302
140. Nem egyenes vonalú csavarfelületek .................................305
141. Több bekezdésű csavarok ...................................................306
142. Transzlációs felületek...............................................306
143. Grafikus felületek ............................................307
144. Burkolófelületek ..............................................................308
XX. Egyenes vonalú felületek...............................310
145. A kiteríthető felületekről általában ............................................310
146. Kúp, henger és síkidomok összetételéből kialakított kiteríthető felületek............311
147. Két görbével megadott kiteríthető felületek................................................313
148. Torzfelületek származtatása .........................................314
149. Algebrai és transzcendens torzfelületek..........................315
XXI. Másodrendű felületek.....................................318
150. A felületekről általában, osztályozásuk....................................318
151. Az ellipszoid ......................................................... 320
152. Kétköpenyű hiperboloid ....................................................321
153. Egyköpenyű hiperboloid ....................................................................322
154. Elliptikus paraboloid ..........................................324
155. Hiperbolikus paraboloid .......................................325
156. A kúp......................................................................326
157. A henger......................................327
158. Két másodrendű felület térbeli affinitása ...........................328
HARMADIK RÉSZ
A MÉRŐSZÁMOS ÁBRÁZOLÁS ALAPJAI
XXII. Térelemek ábrázolása...................................331
159. Bevezetés, méretarány, lépték................................331
160. A pont ábrázolása .................................................... 333
161. Az egyenes ábrázolása és graduálása.............................334
162. Az egyenes lejtője és rézsűje ...............................336
163. Két egyenes viszonylagos helyzetei ...............................338
164. A sík ábrázolása...................................................... 340
XXIII. Térelemek helyzet- és méretgeometriája.............................341
165. Illeszkedés és összekötés ...........................................342
166. Két sík, továbbá sík és egyenes metszése .........................................343
167. Sík leforgatása szintsíkba .......................................345
168. Egymásra merőleges térelemek ábrázolása................................347
169. Távolság-alapfeladatok ..........................................................348
170. Szög-alapfeladatok....................................349
171. A dőléskúp................................................................................350
XXIV. Összekötések szerkesztése.....................................351
172. Az összekötésekről általában ................................................352
173. Adott ponton átmenő összekötés . .............................................353
174. Adott iránnyal párhuzamos összekötés.............................................354
175. Adott síkkal párhuzamos legrövidebb összekötés........................356
176. Adott dőlésszögű összekötés............................................357
177. Méretelőírásnak megfelelő összekötések............................357
178. Három szintes tengely legrövidebb összekötése...................358
XXV. Vetőmegoldás...........................................360
179. A különféle vetőkről .......................................................360
180. Az egyenes vető megoldása......................................361
181. A forgatóvető megoldása...........................................364
GÖRBE VONALAK ÉS GÖRBE FELÜLETEK
XXVI. Egyszerű görbe vonalak és felületek..................................... 367
182. Sík- és térgörbe..............................................................................367
183. Egyszerű felületek............................371
184. Egyszerű védőpillér szerkesztése...................................................372
185. Bányaüzemi építmény védőpillére ..............................374
XXVII. Terep- és rézsűfelületek.............................377
186. A terepfelület ábrázolása...................................377
187. A terepfelület lejtvonala...................................380
188. Terepfelület metszése síkkal és egyenessel..................................................................382
189. Rézsűfelületek............................................................................384
190. Csavarvonalra szerkesztett rézsűfelületek...........................386
XXVIII. Szerkesztések a terepfelületen..............................388
191. Táró külszíni pontjának felkeresése...................................... 389
192. Telep kibúvásának szerkesztése ......................................... 390
193. összetett rézsűfelület és terep metszése................................... 392
194. Terepfelület látrajza ................................................... 394
NEGYEDIK RÉSZ
KÚPSZELETEK SZERKESZTÉSE PROJEKTÍV MŰVELETTEL
195. A kúpszeletek polaritása .................................395
196. Brianchon és Pascal tétele.......................................397
197. Szerkesztések Pascal-egyenessel és Brianchon-ponttal .................399
Ajánlott irodalom...........................................................403
Név- és tárgymutató....................................................405
Dr. Petrich Géza
Dr. Petrich Géza műveinek az Antikvarium.hu-n kapható vagy előjegyezhető listáját itt tekintheti meg: Dr. Petrich Géza könyvek, művekMegvásárolható példányok
Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.