1.062.618
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát

VISSZA
A TETEJÉRE
JAVASLATOKÉszre-
vételek
Numerikus analízis
Kézirat
| Kiadó: | Tankönyvkiadó Vállalat |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Ragasztott papírkötés |
| Oldalszám: | 394 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 24 cm x 17 cm |
| ISBN: | |
| Megjegyzés: | Tankönyvi szám: J 4-883. Kézirat. Fekete-fehér ábrákkal illusztrálva. Példányszám: 205. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Előszó
Ez a jegyzet a III. éves matematikus mérnök szakos hallgatók Numerikus analízis című tantárgyának programja szerinti válogatásban tárgyalja az előírt tananyagot. Ez magyarázza, hogy a tárgykörök... TovábbElőszó
Ez a jegyzet a III. éves matematikus mérnök szakos hallgatók Numerikus analízis című tantárgyának programja szerinti válogatásban tárgyalja az előírt tananyagot. Ez magyarázza, hogy a tárgykörök közül miért éppen ezek kerültek tárgyalásra, és igen sok minden maradt a váltogatáson kívül. Az igényesebb olvasó tájékoztatására bőséges irodalomjegyzéket csatoltam a jegyzetemhez. Itt felsoroltam mindazokat a műveket, amelyeket felhasználtam, illetve amelyek megítélésem szerint alkalmasak arra, hogy a szükséges bővítések, kiegészítések tekintetében kellően eligazítsanak. Első olvasásra bizonyára azonnal feltűnik, hogy a jegyzet csak elvétve tartalmaz példákat, illetve egyáltalán nem tartalmaz feladatokat. Ezt a hiányosságot egy készülő példatár fogja megszüntetni.Budapest, 1977. VII. 20
Dr. Bajcsay Pál Vissza
Tartalom
| Előszó | 3 |
| Függvényközelitések | 5 |
| Interpoláció | 7 |
| A közönséges interpoláció problémája | 7 |
| Interpoláció polinommal | 9 |
| Lagrange-féle interpolációs polinom | 11 |
| Egyenközü alappontabszcisszák esete | 13 |
| Newton-féle interpolációs polinom | 14 |
| Egyenközü alappontabszcisszák esete | 15 |
| Interpolációs polinom hibája | 19 |
| Lineáris interpoláció hibája | 22 |
| Hermite-féle interpoláció | 23 |
| Interpolációharmadfoku spline-függvényekkel | 26 |
| Valós kétváltozós interpoláció polinommal | 38 |
| Numerikus deriválás és integrálás | 44 |
| A differenciálszámitás operátorai | 44 |
| Numerikus deriválás | 48 |
| Numerikus integrálás | 54 |
| Trapéz-formula | 57 |
| Simpson-formula | 59 |
| Newton-féle "3/8-os" formula | 61 |
| Szimmetrikus 4-lépéses formula | 63 |
| Richardson módszere a hibabecslésre és az integrál közelitő értékének javitására | 65 |
| Néhány lehetőség improprius integrálok közelitő numerikus kiszámitására | 67 |
| Kettős integrál numerikus kiszámitása | 70 |
| Függvényközelités a legkisebb négyzetek módszerével diszkrét pontokban | 73 |
| A feladat kitüzése és megoldása | 73 |
| Kiegyenlités polinommal | 77 |
| Kiegyenlités a legkisebb négyzetek módszerével ortogonalizálás utján | 80 |
| Empirikus formulák közelitő előállitása linearizálás utáni kiegyenlitéssel | 83 |
| Négyzetes legjobb közelités adott intervallumban | 86 |
| Függvényrendszer lineáris függése, illetve függetlensége | 86 |
| Intervallumban négyzetes legjobb közelités | 91 |
| Négyzetes legjobban közelitő polinom | 94 |
| Ortogonális bázis-függvényrendszer megválasztása | 96 |
| Schmidt-féle ortoganalizálási eljárás | 99 |
| Ortogonális polinomrendszerek | 101 |
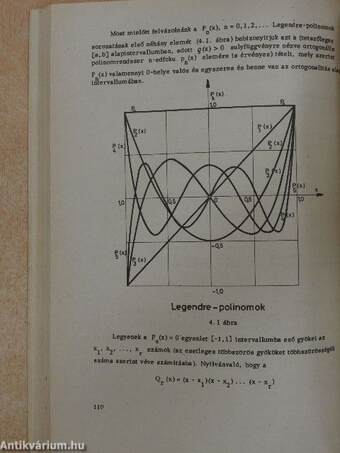
| Legendre-polinomok | 104 |
| Négyzetes legjobb közelités Legendre-polinomokkal | 111 |
| Trigonometrikus interpoláció | 115 |
| Elsőfaju Csebisev-polinomok | 122 |
| Négyzetes legjobb közelités Csebisev-polinomokkal | 129 |
| Intervallumban megközelitőleg legjobb polinomközelitések | 133 |
| Egyenletek közelitő megoldása | 137 |
| f(x) = 0 alaku egyenletek | 139 |
| Sorozatos intervallum felezés | 139 |
| Hurmódszer vagy szelőmódszer (regula falsi) | 141 |
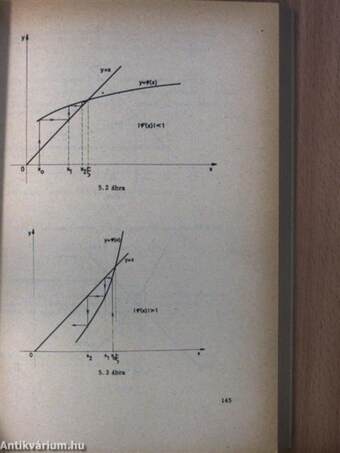
| Iteráció (sorozatos közelités) | 143 |
| Newton módszere (érintőmódszer) | 147 |
| Algebrai egyenletek közelitő megoldása | 156 |
| Algeberai egyenlet gyökei abszolut értékének felső, illetve alsó korlátja | 156 |
| Algebrai egyenlet gyökei többszörösségének a megszüntetése | 158 |
| Egyszeres valós gyökök számának meghatározása Sturm tétele alapján | 160 |
| Horner-féle elrendezés | 164 |
| Ruffini-Horner-féle eljárás | 170 |
| A Horner-féle elrendezés általánositása valós együtthatóju komplex változós polinom esetén | 171 |
| Bairstow módszere konjugált komplex gyökpár meghatározására | 173 |
| Rutishauser módszere: hányados-különbség- (QD) algoritmus | 176 |
| Nemlineáris egyenletrendszerek közelitő megoldása | 181 |
| Iteráció (sorozatos közelités) | 181 |
| A Newton-féle iteráció általánositása | 190 |
| A gradiens-módszer alapgondolata | 193 |
| Lineáris egyenletrendszerek | 197 |
| Lineáris egyenletrendszerek megoldásának problémája | 197 |
| n-ismeretlenes n inhomogén lineáris egyenletből álló egyenletrendszer dierkt megoldása | 201 |
| Az inver mátrix meghatározása elemi sor-átalakitások utján | 202 |
| Blokkokra particionált kvadratikus mátrix invertálása rekurzióval | 205 |
| Általános, (n.m)-tipusu mátrix rangja | 210 |
| Zérustól különböző kvadratikus diád (elsőrangu mátrix) normálalakja | 218 |
| Mátrix bázisfaktorizációja. minimális diádösszegre bontása | 221 |
| Bázisfaktorizáció alkalmazása homogén lineáris egyenletrendszer megoldására | 229 |
| Projektor (idempotens) mátrixok néhány tulajdonsága | 233 |
| E. W. Purcell un. vektormódszere homogén lineáris egyenletrendszer direkt megoldására | 240 |
| Projektor mátrixok alkalmazása homogén lineiáris egyenletrendszerek direkt megoldására | 247 |
| Ortogonalizálási eljáráshomogén lineáris egyenletrendszer direkt megoldására | 254 |
| A báziscsere módszerrel ekvivalens algoritmus | 261 |
| Diáddal módositott nem-szinguláris kvadratikus mátrix inverze | 272 |
| Közelitő mátrixok inverze, közelitő egyenletrendszerek megoldása | 273 |
| Kvadratikus alak pozitiv definit voltának kritériumairól | 278 |
| Lineáris egyenletrendszerek iterációs megoldása | 290 |
| A Jacobi- és a Gauss-Seidel-féle iteráció | 292 |
| Iteráció a hibavektorok minimizálása utján | 294 |
| Relaxációs módszerek | 296 |
| Kvadratikus mátrix sajátérték-, sajátvektor problémája | 303 |
| Kvadratikus mátrix sajátértékeinek, sajátvektorainak a meghatározása | 305 |
| A sajátérték-, sajátvektor-probléma | 305 |
| Karakterisztikus polinom előállitása Fagyejev módszerével | 311 |
| Minimál polinom | 318 |
| Lineárisan független sajátvektorok száma | 322 |
| Kvadratikus mátrix minimálpolinomjának meghatározása alkalmas Krilov-féle sorozattal | 332 |
| Sajátértékek, sajátvektorok meghatározása iterációval (Mises módszere) | 340 |
| Közelitő sajátértékek, sajátvektorok javitása | 348 |
| Kvadratikus mátrix analitikus függvényének redukálása minimális fokszámu mátrixpolinomra | 351 |
| Differenciálegyenletek közelitő megoldása | 355 |
| Közönséges differenciálegyenletek kezdetiérték-feladata | 357 |
| Közelitő megoldás sorozatos közelitéssel (szukcessziv approximációval) | 357 |
| Sorozatos közelités homogén lineáris differenciálegyenlet-rendszer esetén | 359 |
| Nem lineáris differenciálegyenletrendszer iterációs megoldása linearizálás utján | 362 |
| Megoldás hatványsor alakjában | 365 |
| Az Euler-Cauchy-féle törtvonalmódszer és különféle javitásai | 367 |
| A Runge-Kutta-féle közelitő eljárás | 369 |
| Másodrendü lineáris differenciálegyenlet peremérték-feladata | 378 |
| A peremérték-feladat visszavezetése kezdetiérték-feladatra | 378 |
| A véges differenciák módszere | 380 |
| A próbafüggvények módszere | 382 |
| Felhasznált és ajánlott irodalom | 385 |
| Tartalomjegyzék | 391 |
Dr. Bajcsay Pál
Dr. Bajcsay Pál műveinek az Antikvarium.hu-n kapható vagy előjegyezhető listáját itt tekintheti meg: Dr. Bajcsay Pál könyvek, művekMegvásárolható példányok
Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.