1.067.694
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát

VISSZA
A TETEJÉRE
JAVASLATOKÉszre-
vételek
A valószínűségszámítás és gyakorlati alkalmazásai
| Kiadó: | Dacia Könyvkiadó |
|---|---|
| Kiadás helye: | Kolozsvár |
| Kiadás éve: | |
| Kötés típusa: | Fűzött kemény papírkötés |
| Oldalszám: | 350 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 21 cm x 15 cm |
| ISBN: | |
| Megjegyzés: | Fekete fehér ábrákkal illusztrálva. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Tartalom
| Előszó | 5 |
| Bevezetés | 7 |
| Alapfogalmak | 11 |
| A valószínűségszámítás tárgya | 11 |
| Kísérlet, események | 11 |
| Eseményalgebra | 13 |
| Eseményalgebrák fontosabb összefüggései, tételei | 15 |
| Példák | 18 |
| Feladatok | 22 |
| A valószínűség fogalma | 23 |
| Abszolút és relatív gyakoriság. A valószínűség fogalma | 23 |
| A valószínűségek axiómái. Kolmogorov elmélete | 24 |
| Valószínűségek közötti egyszerűbb összefüggések | 26 |
| Példák | 28 |
| Feladatok | 30 |
| Valószínűségek meghatározási módjai | 31 |
| Statisztikai meghatározási mód | 31 |
| Klasszikus meghatározási mód | 31 |
| Példák | 47 |
| Feladatok | 49 |
| Feltételes valószínűség és események függetlensége | 50 |
| A feltételes relatív gyakoriság és a feltételes valószínűség fogalma | 50 |
| A valószínűségek szorzási szabálya | 52 |
| Események függetlensége | 52 |
| A teljes valószínűség tétele. A Bayes-féle képlet | 55 |
| Példák | 56 |
| Feladatok | 59 |
| Valószínűségi változók, eloszlás- és sűrűségfüggvények | 61 |
| Valószínűségi változók | 61 |
| Valószínűségi változó értelmezése | 61 |
| Valószínűségeloszlások értelmezése | 62 |
| Eloszlás- és sűrűségfüggvények | 65 |
| Eloszlásfüggvény értelmezése | 65 |
| Sűrűségfüggvény értelmezése és tulajdonságai | 67 |
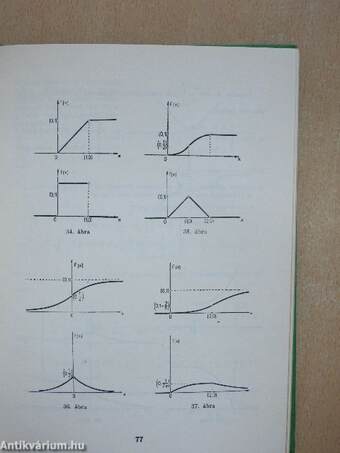
| Az eloszlásfüggvény és a sűrűségfüggvény grafikus képei | 69 |
| Valószínűségi változó függvényeinek eloszlásfüggvénye, illetőleg sűrűségfüggvénye | 72 |
| Példák | 73 |
| Feladatok | 82 |
| Többdimenzós valószínűségeloszlások | 83 |
| Valószínűségi vektorváltozók | 83 |
| Két valószínűségi változó együttes eloszlása | 84 |
| Többdimenziós valószínűségeloszlások | 88 |
| Feltételes valószínűségeloszlások | 89 |
| Valószínűségi változók függetlensége | 91 |
| Független valószínűségi változókkal végzett műveletek | 92 |
| Példák | 96 |
| Feladatok | 111 |
| Leggyakrabban előforduló valószínűségeloszlások, eloszlás- és sűrűségfüggvények | 113 |
| Diszkrét eloszlások | 113 |
| Egyenletes eloszlás | 113 |
| Egyszerű alternatíva | 113 |
| Binomiális vagy Bernoulli-féle eloszlás | 114 |
| Polinomiális eloszlás | 115 |
| Hipergeometrikus eloszlás | 116 |
| Polihipergeometrikus eloszlás | 116 |
| Geometriai eloszlás | 117 |
| Negatív binomiális eloszlás | 117 |
| Poisson-féle eloszlás | 119 |
| Folytonos valószínűségelosztások | 121 |
| Egyenletes eloszlás | 121 |
| Exponenciális eloszlás | 123 |
| Gamma-eloszlások | 126 |
| Normális vagy Gauss-féle eloszlás | 128 |
| A Pearson-féle hi-négyzet eloszlás | 135 |
| A Student-féle "t" eloszlás | 138 |
| Egyéb folytonos eloszlások | 141 |
| Példák, feladatok, táblázatok használata | 143 |
| Példák diszkrét eloszlásokkal | 143 |
| Példák folytonos eloszlásokkal | 146 |
| Feladatok | 150 |
| Valószínűségi változók és valószínűségeloszlások jellemző adatai. Generátor- és karakterisztikus függvények | 152 |
| Valószínűségi változók várható értéke | 152 |
| Diszkrét valószínűségi változók várható értéke | 152 |
| Folytonos valószínűségi változók várható értéke | 153 |
| A várható érték főbb tulajdonságai | 154 |
| A feltételes várható érték fogalma | 157 |
| Valószínűségi változók szórása | 159 |
| Valószínűségi változók szórásának értelmezése | 159 |
| A szórás főbb tulajdonságai | 161 |
| A Csebisev-féle egyenlőtlenség | 162 |
| Valószínűségi változók momentumai és centrális momentumai | 164 |
| Momentumok | 164 |
| Centrális momentumok | 164 |
| Valószínűségi változók egyéb jellemző adatai | 165 |
| A medián | 165 |
| A módusz | 165 |
| Sűrűségfüggvény ferdültsége és lapultsága | 166 |
| Valószínűségi változók kovarianciája és korrelációja | 167 |
| Kovariancia | 167 |
| Korrelációs együttható | 168 |
| A kovariancia- és a korreláció-mátric | 170 |
| A generátor- és a karakterisztikus függvény | 170 |
| A generátor-függvény | 170 |
| A karakterisztikus függvény | 173 |
| A karakterisztikus függvény tulajdonságai | 174 |
| A legfontosabb valószínűségeloszlások jellemző adatainak kiszámítása, illetőleg meghatározása | 176 |
| Diszkrét eloszlások | 176 |
| Folytonos eloszlások | 181 |
| Példák és feladatok | 188 |
| Példák | 188 |
| Feladatok | 193 |
| A nagy számok törvényei | 196 |
| Néhány elvi kérdés tisztázása | 196 |
| A nagy számok törvényének Bernoulli-féle és Csebisev-féle alakja | 197 |
| A sztochasztikus konvergencia fogalma | 197 |
| Bernoulli tétele a relatív gyakoriság és a valószínűség kapcsolatáról | 197 |
| A nagy számok törvényének Csebisev-féle alakja | 198 |
| A nagy számok törvényének egyéb alakjai | 199 |
| A nagy számok törvényének Markov-féle alakja | 199 |
| A nagy számok törvényének Hincsin-féle alakja | 199 |
| Bernstein tétele | 200 |
| A nagy számok erős törvényei | 200 |
| Konvergencia 1 valószínűséggel | 200 |
| A nagy számok erős törvényének néhány változata | 201 |
| A ngy számok törvbényének gyakorlati alkalmazásairól | 202 |
| Két sajátos egyenlőtlenség | 202 |
| Adott pontossággal előírt közelítésekhez szükséges kísérletek számának meghatározása | 203 |
| Példák | 205 |
| Határeloszlás-tételek | 207 |
| A központi határeloszlás tétele | 207 |
| Moivre-Laplace tétel | 209 |
| Ljapunov tétele | 209 |
| A határeloszlás tételek alkalmazása | 210 |
| Sztochatsztikus folyamatok | 212 |
| A Markov-féle láncok elmélete | 212 |
| A Markov-lánc értelmezése | 212 |
| Homogén Markov-láncok | 213 |
| Markov-láncok ergodicitása | 216 |
| Markovtétele | 217 |
| Példák | 217 |
| Feladatok | 224 |
| Folytonos állapothatározójú Markov-láncok | 225 |
| Sztochasztikus folyamatok | 227 |
| Markov-folyamatok értelmezése | 227 |
| A Poisson-folyamat értelmezése | 229 |
| Születési és halálozási folyamat | 233 |
| Példák | 236 |
| Feladatok | 240 |
| A matematikai statisztika elemei | 241 |
| Statisztikai sokaság és statisztikai minták | 241 |
| Statisztikai sokaság fogalma | 241 |
| Minta és mintavétel statisztikai sokaságból | 243 |
| Rendezett minták és empírikus eloszlásfüggvény | 243 |
| Az empírikus várható érték és az empírikus szórásnégyzet | 245 |
| Statisztikai becslések | 246 |
| Statisztikai becslések fajtái | 246 |
| A várható érték és a szórásnégyzet becslései | 247 |
| Konfidencia-intervallumok | 249 |
| Példák | 254 |
| Statisztikai próbák | 256 |
| Illeszkedésvizsgálat | 264 |
| Illeszkedésvizsgálat grafikus módszerekkel | 264 |
| A "x2" próba | 265 |
| A Kolmogorov-féle próba | 269 |
| Példák | 269 |
| Valószínűségi változók kapcsolatának vizsgálata | 274 |
| Regressziók | 274 |
| Lineáris regressziók | 275 |
| Példák | 279 |
| A valószínűségszámítás alkalmazása néhány fontosabb szakterületen | 283 |
| Alkalmazások a természettudományok keretében | 283 |
| Alkalmazások a fizikában | 283 |
| Alkalmazások a kémiában, biológiában és orvostudományokban | 288 |
| Alkalmazások a telefontechnikában | 290 |
| Alkalmazások a matematikában | 291 |
| Alkalmazások a gazdaságtudományokban és az iparban | 295 |
| Várakozási (sorbanállási) feladatok | 295 |
| Készletgazdálkodási feladatok | 301 |
| Különböző ipari alkalmazások | 303 |
| Üzembiztonsági számítások | 305 |
| Rövid történeti áttekintés | 308 |
| Feladatok megoldásai, útmutatások | 313 |
| Táblázatok | |
| A binomiális együtthatók táblázata | 326 |
| A Poisson-eloszlás táblázata | 328 |
| A nem teljes gamma-függvény táblázata | 332 |
| Az N (0,1) eloszlás sűrűségfüggvényének táblázata | 336 |
| Az N(0,1) eloszlás eloszlásfüggvényének táblázata | 338 |
| Táblázat a x2 próba használatához | 340 |
| Táblázat a Student-féle "t" próbához | 341 |
| Felhasznált és ajánlott könyvészeti anyag | 344 |
Témakörök
Cseke Vilmos
Cseke Vilmos műveinek az Antikvarium.hu-n kapható vagy előjegyezhető listáját itt tekintheti meg: Cseke Vilmos könyvek, művekMegvásárolható példányok
Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.