1.067.308
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát

VISSZA
A TETEJÉRE
JAVASLATOKÉszre-
vételek
Bevezetés a matematikába
Kézirat/Egységes jegyzet/Eötvös Loránd Tudományegyetem Természettudományi Kar
| Kiadó: | Tankönyvkiadó |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Ragasztott papírkötés |
| Oldalszám: | 287 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 24 cm x 17 cm |
| ISBN: | |
| Megjegyzés: | Kézirat. 500 példányban jelent meg. Tankönyvi száma: J 3-1009. 28 fekete-fehér ábrával illusztrálva. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Előszó
Részlet:E jegyzet programozó-matematikus hallgatók számára készült. Azokat az alapvető matematikai ismereteket tartalmazza, amelyek a matematika különböző fejezeteinek megértését lehetővé teszik.... Tovább
Előszó
Részlet:E jegyzet programozó-matematikus hallgatók számára készült. Azokat az alapvető matematikai ismereteket tartalmazza, amelyek a matematika különböző fejezeteinek megértését lehetővé teszik. A feldolgozott anyag bepillantást nyújt a számítástechnika elméleti megalapozását szolgáló matematikai fejezetekbe is.
A jegyzet megírásánál alapoztunk a hallgató középiskolában szerzett ismereteire is. Ez lehetővé tette egyes anyagrészek tömör kifejtését (pl. kombinatorika), másrészt azt, hogy egyes fogalmakat példaként megemlítsünk, mielőtt még ezek mélyebb kifejtésére rátérnénk. így beszélünk az I. Fejezetben valós számok rendezéséről (a középiskolás ismeretekre támaszkodva), míg a valós számok axiomatikus bevezetését a következő fejezetben tárgyaljuk.
A tárgyalt anyagrészeknél több könyvre támaszkodtunk. A IX. Fejezet kifejtése lényegileg E. Mendelson: Introduction to Mathematical Logic című könyve alapján történik. Vissza
Tartalom
BEVEZETÉS 5I Fejezet. Alapfogalmak 7
1. Halmazok, halmazműveletek 7
2. Ítéletek, ítéletműveletek 15
3. Relációk, függvények 24
Feladatok 39
I. Fejezet. A számfogalom bővítése 42
1.Természetes számok, egész számok 42
2. Racionális számok 49
3. Valós számok 51
4. Komplex számok 58
Feladatok 66
III. Fejezet. Számelméleti alapismeretek 67
1. Oszthatóság . . . 67
2. Primszámok 74
3. Kongruenciák 77
4. Multiplikatív számelméleti függvények 82
5. Számrendszerek 89
Feladatok 92
IV. Fejezet. Kombinatorika 96
1. Alapfeladatok 96
2. Binomiális és polinomiális tétel 101
3. Logikai formula 104
Feladatok 106
V. Fejezet. Halmazok számossága 109
1. § Megszámlálható számossága halmazok 109
2. § Nem megszámlálható halmazok 115
3. § Halmazok számosságának összehasonlítása 120
Feladatok 129
VI. Fejezet. Algebrai struktúrák 131
1. Művelet 131
2. Struktúra 135
3. Félcsoport 135
4. Csoport 137
5. Csoport felbontása mellékosztályokra. Invariáns részcsoport 141
6. Izomorfizmus, homomorfizmus 143
7. Permutáció-csoport 144
8. Gyűrű 147
9. Ideál 148
10. Egységelemes integritási tartomány. Euklideszi gyűrű . . . 150
11. Test . . . 155
12. Polinomgyűrű 156
13. Szimmetrikus polinomok alaptétele 163
14. Az algebra alaptétele és következményei 169
15. Racionális függvények teste 171
16. A primmodulusu kongruenciák teste feletti polinomgyűrű 174
Feladatok 175
VII. Fejezet. Boole-algebrák, -függvények, -formák 179
1. A Boole-algebra fogalma 179
2. Boole-függvények és Boole-formák 184
3. A Boole-algebra alkalmazásai 194
Feladatok . 202
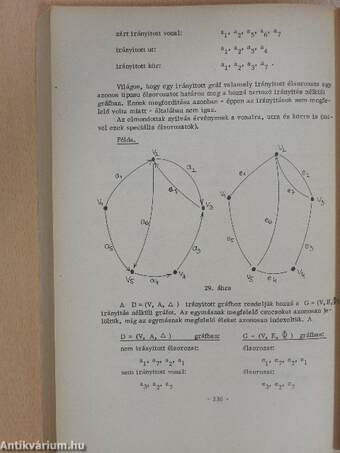
VI. Fejezet. Gráfok 204
1. Irányítás nélküli gráfok 204
2. Irányított gráfok 229
Feladatok 244
IX. Fejezet. Rekurzív függvények, Markov algoritmusok,
Turing gépek 246
1. Rekurzív függvények . 246
2. Markov algoritmusok 252
3. Turing gépek 273
Feladatok 287
Megvásárolható példányok
Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.