1.068.031
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát

VISSZA
A TETEJÉRE
JAVASLATOKÉszre-
vételek
A statisztikai matematika alapjai
Könnyűipari Minisztérium Munkaügyi és Oktatási Főosztálya/Kézirat
| Kiadó: | Könnyűipari Minisztérium Munkaügyi és Oktatási Főosztály-Könnyüipari Szervezési Intézet |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Fűzött papírkötés |
| Oldalszám: | 192 oldal |
| Sorozatcím: | Segédlet |
| Kötetszám: | 3 |
| Nyelv: | Magyar |
| Méret: | 20 cm x 14 cm |
| ISBN: | |
| Megjegyzés: | Kézirat. 700 példányban jelent meg. Néhány fekete-fehér ábrával. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Előszó
A fizikai világ és a társadalom mozgásai objektíve jelenségekben nyilvánulnak meg. Jelenségen olyan, a megismerés számára körülhatárolható folyamatot értünk, amely adott körülmények között... TovábbElőszó
A fizikai világ és a társadalom mozgásai objektíve jelenségekben nyilvánulnak meg. Jelenségen olyan, a megismerés számára körülhatárolható folyamatot értünk, amely adott körülmények között játszódik le. A jelenségeket a megfigyelés szempontjaitól függően két nagy csoportra, egyedi és nem egyedi jelenségekre oszthatjuk. A nem egyedi jelenségek olyan folyamatok, amelyek többször megismétlődnek. Ez utóbbiak vizsgálata a megismerés és a mindennapi élet számára különösen fontos, mert létezésükről a múltból tudomásunk van, bekövetkezésükre pedig a jövőben számítanunk kell. Ezek közé sorolhatjuk például egy adott földrajzi helyen az időjárási jelenségeket: eső, meghatározott irányú szél, stb. Hozzátesszük mindehhez azt, hogy jelenség mesterséges körülmények között is létrehozható. A nem egyedi jelenségek jelentős része olyan törvényszerűségek szerint játszódik le, amelyek tudományos módszerekkel felderíthetők. A nem egyedi jelenségeknek egy ilyen csoportját alkotják a véletlen tömegjelenségek. A valószínűségszámítás a modern matematikának az az ága, amely a véletlen tömegjelenségeket vizsgálja matematikai eszközökkel. A véletlen tömegjelenség, mint a valószínűségszámítás tárgya, alapfogalom, amelynek jelentését az alábbiakban pontosabban meghatározzuk. VisszaTartalom
BEVEZETÉS 1A VALÓSZÍNŰSÉGSZÁMÍTÁS TÁRGYA ÉS FELADATA 1
A valószínűségszámítás tárgya 1
A véletlen tömegjelenség fogalma 2
A valószínűségszámítás feladata 4
I. A VALÓSZÍNŰSÉGSZÁMÍTÁS ALAPFOGALMAI ÉS SEGÉDESZKÖZEI 5
A véletlen kísérlet fogalma 5
Elemi események 6
Az eseménytér fogalma 7
A halmazelméleti és eseményalgebrai alapfogalmak analógiája 7
A halmaz fogalma 8
Halmazok közötti relációk 10
Az alaphalmaz 11
Véletlen események 11
Műveletek halmazokkal és eseményekkel 13
A valószínűség fogalma a mindennapi beszédben 19
Gyakoriság és relatív gyakoriság 21
A nagy számok tapasztalati törvénye 25
A valószínűség axiómái 25
A valószínűségi mező fogalma 29
A valószínűség alaptételei 29
II. A KLASSZIKUS VALÓSZÍNŰSÉGI MEZŐ. A GEOMETRIAI VALÓSZÍNŰSÉG ELVE 34
A klasszikus valószínűségi mező 34
Alapvető kombinatorikai ismeretek 36
1. Permutációk 37
2. Kombinációk 41
3. Variációk 45
Binomiális tétel és binomiális együtthatók 48
Számítási példák a klasszikus valószínűségi mezőben 49
Mintavétel visszatevés nélkül 57
A geometriai valószínűség elve 58
III. FELTÉTELES VALÓSZÍNŰSÉG. ESEMÉNYEK FÜGGETLENSÉGE 62
Feltételes valószínűség 62
A valószínűségek szorzási szabálya 66
A teljes valószínűség tétele 69
Események függetlensége 71
IV. VALÓSZÍNŰSÉGI VÁLTOZÓK. NEVEZETESEBB ELOSZLÁSOK 72
A valószínűségi változó fogalma 72
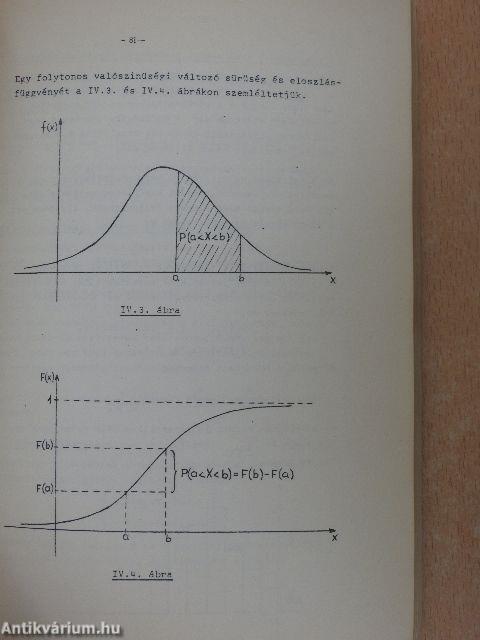
Valószínűségi változók eloszlása és eloszlásfüggvénye 76
A hisztrogram, mint mérési eredmények rögzítési módszere 82
Két valószínűségi változó együttes eloszlása 83
Valószínűségi változók függetlensége 86
Nevezetesebb eloszlások 87
A./ Nevezetesebb diszkrét eloszlások 87
1./ A binomiális eloszlás 87
2./ Poisson eloszlás 88
B./ Nevezetesebb folytonos eloszlások 89
1./ Egyenletes eloszlás 89
2./ Normális eloszlás 90
V. KÖZÉPÉRTÉKEK, SZÓRÁS. ELOSZLÁS ALAKI JELLEMZŐI. VALÓSZÍNŰSÉGI VÁLTOZÓK VÁRHATÓ ÉRTÉKE, SZÓRÁSA. LEÍRÓ STATISZTIKA, MATEMATIKAI STATISZTIKA 93
Középértékek 94
Számtani átlag 95
Négyzetes átlag 98
Harmonikus átlag 99
Helyzeti középértékek 100
Módusz 100
Medián 100
Kvantiliszek 101
Ferdeség 102
Momentumok, lapultság 104
Szórás 105
Az átlag és szórás egyszerűbb kiszámítása 108
Szórásnégyzet felbontása 114
Valószínűségi változók várható értéke, szórása 118
Nevezetes valószínűség eloszlások várható értéke, szórása 122
VI.. KORRELÁCIÓ-SZÁMÍTÁS 126
Korreláció 126
Kétváltozós sokaság sztochasztikus kapcsolata 130
A regressziós függvény 137
Nem lineáris regresszió 141
Parabola illesztése 143
A kapcsolat szorossága 148
Hiperbola illesztése 149
Exponenciális és logaritmikus regressziós görbék 152
Többszörös korreláció 156
Rangkorreláció, asszociáció 156
Rangkorreláció 157
Asszociáció 160
Összefoglalás, megjegyzések 163
VII. MINTAVÉTEL 165
Bevezetés, alapfogalmak 165
Sokasági jellemzők becslése, torzítatlan becslés, standard hiba, konfidencia intervallum 171
Értékösszeg, megoszlási viszonyszám és hányados becslése egyszerű véletlen mintából 180
Mintanagyság megválasztása 188-192
Megvásárolható példányok
Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.