A mathematikai és csillagászati földrajz kézikönyve

Szerző

Dr. Kövesligethy Radó

Szerkesztő

Dr. Lóczy Lajos

Budapest

'Dr. Kövesligethy Radó: A mathematikai és csillagászati földrajz kézikönyve ' összes példány

Kiadó:	Kogutowicz és Társa Magyar Földrajzi Intézete
Kiadás helye:	Budapest
Kiadás éve:	1899
Kötés típusa:	Aranyozott gerincű kiadói vászonkötés
Oldalszám:	911 oldal
Sorozatcím:	A Tudományos Földrajz kézikönyvei
Kötetszám:	1
Nyelv:	Magyar
Méret:	24 cm x 16 cm
ISBN:
Megjegyzés:	320 fekete-fehér szövegközti ábrával illusztrálva. Nyomtatta a Hornyánszky Viktor cs. és kir. udv. könyvnyomdája, Budapest.

Értesítőt kérek a kiadóról

Értesítőt kérek a sorozatról

A beállítást mentettük,
naponta értesítjük a beérkező friss
kiadványokról

Előszó

A szerző előszava

Azon érdeklődésnél fogva, melyet a geographiai tudományok csillagász és physikus körökben ébreszteni képesek voltak, oly hatalmas lépést tettek az exakt tudományok felé és... Tovább

Tartalom

Bevezetés	1
A csillagászati földrajz
Alapvető tanai
A csillagászati földrajz tárgyának felosztása és a sorrend megállapítása
Mathematikai előkészítő	4
Mathematikai repertorium geographusok számára
A mathematika és mechanika mint segédtudomány
Goniometria és trigonometria	5
Goniometriai függvények
Derékszögű síkháromszög megoldása
Complementáris szög goniometriai függvényei
Goniometriai függvények előjelei és ábrázolása
Szögösszeg goniometriai függvényei
Goniometriai függvények szorzatképletei
Goniometriai összegképletek
A kétszeres szög függvényei
Néhány speciális érték
A síkháromszög megoldása
Gömbi háromszögtan	14
A gömbi háromszög megoldása
Derékszögű gömbháromszög megoldása
Logarithmusos transformatio
Oldalösszeg tétele, Gauss egyenletei és Napier analogiái
Gömbi két- és háromszög területe
Logarithmusos számolás	23
A logarithmusos számolás előnyei
Logarithmustábla berendezése
Additio s subtractio logarithmus
Logarithmusos számítás berendezése
Természetes (Napier) logarithmusok
Logarithmusos képletek
Végtelen sorok	29
A végtelen sorok fontossága
A convergentia kriteriumai
A sorok főbb alakjai
Newton binom sora
Exponenses és logarithmusos sorok
Goniometriai sorok
Interpolatio	35
Használata
Graphikus ábrázolása
Egyenletek megoldása	37
Magasabb fokú és transcendes egyenletek numerikus megoldása és graphikus ábrázolása
Regula falsi
Empirikus képletek	38
Hatványsorok
Periodicus sorok; Fourier-féle sor
Fourier-féle sinus-sor
Fourier-féle cosinus-sor
Fourier-féle teljes sor
Infinitesimális számítás	51
Az infinitesimális számítás mibenléte
Részei
Használata
Függvények és ábrázolásuk	52
A függvény fogalmának meghatározása
A független és a függőváltozó
Ábrázolásai
Differentiatio	53
"Natura non facit saltum"
A differentiatio
A differentiálquotiens jelentősége
Taylor és Mac-Laurin-féle sor
Integratio	57
Az integratio mibenléte
Az integratio geometriai ábrázolása
Az integrál geometriai ábrázolása
Használata
Mechanikai integratio	59
Integratiós formulák
Simpson-féle formula
Használatuk
Curveometer és planimeter	62
Integrograph műszerek
Curveometer
Planimeter
E műszerek leírása és használatuk módja
Közelítő rectificatio és quadratura	81
A közelítő rectificatio (kiegyenesítés) és a közelítő (quadratura (területmeghatározás) mibenléte
Geometriai helymeghatározás	84
Helymeghatározás a vonalon
Helymeghatározás a lapon
Coordinátarendszerek
Helymeghatározás a térképen
Helymeghatározás a glóbusokon és a Föld felületén
Helymeghatározás a térben
Térbeli coordinátarendszerek
Coordinátarendszerek transformatiója
A napi mozgás
Az éggömb	98
A csillagos ég szerepe a csillagászati geographiában
Az éggömb és az égboltozat
Az álló csillagok napi mozgása	100
A csillagos ég látszólagos mozgása
A horizont coordinátarendszere
Az aequator coordinátarendszere
Iv és idő átváltozása
A két rendszer egyesítése
Geographiai szélesség
Geographiai hosszúság
A geographiai hosszkülönbségek jelentése
A csillagok nappali és éjjeli íve
A holdpálya fekvése	277
A holdpálya fekvésének meghatározása
A holdpálya csomóinak hátrálása
Változások
A holdpálya alakja. Anomalistikus hónap	283
A holdpálya alakjának meghatározása
Az anomalistikus hónap tartama
A különböző holdperiodusok összehasonlítása	284
A Hold keringési ideje más-más kezdőpontra vonatkoztatva
Összehasonlító táblázatok
A Hold relativ mozgása
A Hold mozgásának egyenlőtlenségei	285
A középponti egyenlítés
Az evectio
A variatio
Az évi egyenlítés
Egyéb egyenlőtlenségek
A Hold valódi helyének kiszámítása egy példán bemutatva
Fogyatkozások	293
A fogyatkozások oka és nemei
Teljes árnyék és félárnyék
A Föld vagy Hold árnyékkúpja
Napfogyatkozások	295
A napfogyatkozás létrejöttének körülményei
A napfogyatkozás nemei
A fogyatkozás tartama
A Hold árnyékának metszése a Földdel
Fogyatkozási határok	299
A fogyatkozás határai
Részleges napfogyatkozás határa
Teljes napfogyatkozás határa
Gyűrűs napfogyatkozás határa
Átnézetes táblázat
Holdfogyatkozások	304
A holdfogyatkozás létrejöttének körülményei
Az árnyékkör
A láthatóság kriteriumai
Fogyatkozási határok	306
A fogyatkozási határok kiszámítása
Részleges holdfogyatkozás határa
Teljes holdfogyatkozás határa
Átnézetes táblázat
A centrális holdfogyatkozás közepes tartama
A hold- és napfogyatkozások kiszámítása	307
A hold- és napfogyatkozás idejének közelebbi meghatározása ephemerida-gyűjtemény segítségével
Az eljárás történeti fogyatkozásoknál
Pingré: Art de verifier les dates és Oppolzer: Canon der Finsternisse czímű munkája
A napfogyatkozások ikonographiája
Egy hold- és egy napfogyatkozás teljes kiszámítása graphikai módon
A hold- és napfogyatkozás láthatósági viszonyainak meghatározása földglóbus segítségével
Nap- és holdfogyatkozások összehasonlítása	318
A nap- és holdfogyatkozások számának és láthatóságának összehasonlítása
A fogyatkozások visszatérése. Fogyatkozási cyclusok	319
A cyclikus számítás értéke
A napfogyatkozások visszatérése
A holdfogyatkozások visszatérése
Ugyanazon év nap- és holdfogyatkozásainak összehasonlítása
Egymásra következő évek nap- és holdfogyatkozásainak összehasonlítása
Fogyatkozási periodusok; Saros	328
Fogyatkozási periodusok meghatározása
Saros
A fogyatkozások belépése és kimaradása
A Hold libratiója	331
A Hold tengelyforgása és keringése
A libratio
Hosszúsági libratio
Szélességi librátio
Parallaktikus vagy napi libratio
Physikai libratio
A föld mozgása a térben	336
A régiek felfogása
A primum mobile
Coppernicus magyarázata
Geographiai fogalmak változása
A Föld forgásának bizonyítékai
A mozgás eltéritése a forgó Földön
Az eltérítés nagysága
A Föld lapultsága
Foucault-féle ingakisérlet
Egyéb bizonyítékok
A Föld forgási tengelyének magatartása és a tengelyforgás tartama
A bolygók látszó mozgása	350
A régiek megfigyeléseinek és elmélkedéseinek fontossága
A Nap, Hold és a többi bolygók látszó mozgása
A bolygókeringés második egyenlőtlensége
Az aequatori és ekliptikalis conjunctio
Felső vagy külső, belső vagy alsó együttállás
A Mercur és a Vénus phasisai
A bolygók távolsági viszonyai
A Mercur és Mars látszó pályájának alakja ábrákon bemutatva
Legnagyobb elongatio kiszámítása
A bolygómozgás magyarázata	359
Endoxus-féle rendszer
A Hipparchos-Ptolomaeus-féle epicyclikus mozgás
Ptolomaeus-féle rendszer
Herakleides Pontikos-féle vagy aegyptusi rendszer
Coppernicus-féle rendszer
A belső és külső bolygók direct és retograd mozgásának magyarázata
A Ptolomeus és a Coppernicus-féle rendszer összehasonlitása és relativ értéke
A heliocentrumos rendszer következményei	368
Az állócsillagok évi parallaxisa
Az aberratio	372
Az állócsillagok aberratiója
Az aberratio magyarázata
Az aberratio állandója
A fény véges terjedési sebessége
A hullócsillagok napi gyakorisága
A Coppernicus-féle rendszer egyéb bizonyítékai
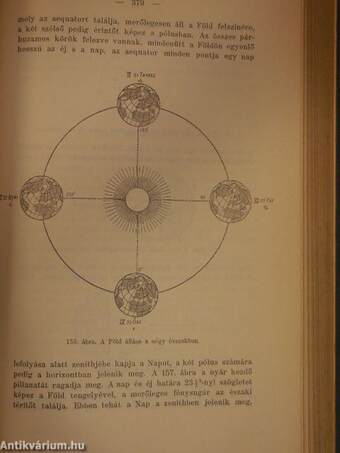
Az évszakok és övök keletkezése Coppernicus szerint	378
A Föld állása és megvilágítása a négy évszakban
Az égitestek távolságai. Parallaxis	381
Az égi testek távolságának meghatározása a parallaxis segítségével
Közeli égi testek parallaxisának meghatározása
A Hold aequatori horizontális parallaxisának kiszámítása
Aristarchos eljárása a Nap parallaxisának meghatározására
A Nap parallaxisának meghatározása a Mars bolygó segítségével
A Vénus-átvonulás
A Nap parallaxisának meghatározása a Vénus-átvonulás segítségével
Delisle módszere a Nap parallaxisának meghatározására
A napparallaxis értéke
A Vénus-átvonulások feltételei	397
A Vénus-átvonulás létrejöttének feltételei
A Vénus-átvonulás visszatérésének periodusai
Közvetett módszerek a napparallaxis meghatározására	400
A napparallaxis meghatározása a Hold mozgásának tekintetbe vételével
A Nap parallaxisának levezetése a földfelületi nehézségi gyorsulásból
Egyéb módszerek
A napparallaxis legvalószinűbb értéke
A Nap távolsága a Földtől
A Nap pályasebességére, pályájára, nagyságára stb. vonatkozó adatok
A naptár. Időszámítás	404
Az időszámítás gyakorlati egységei
A különböző időszámítások kúszált voltának magyarázata
A régiek chronologiája
A csillag heliákus és akronyktikus kelte
A csillag heliákus és kosmikus lenyugvása
A tropikus év és a synodikus hó viszonya
Az aranyszám
Az epakta
Az aranyszám és epakta közötti összefüggés
A vasárnapi betű
A napkör
Mohammedán időszámítás
Időszámítás a görögöknél és a rómaiknál
Júliusi naptár
Gregori naptár
Aegyptusi naptár
A babyloniak és a chaldaeusok időszámítása
A zsidók időszámítása
A khinai időszámítás
A Föld
A Föld ideális alakja és méretei	423
A Föld gömbalakja
Bizonyítékok a Föld gömbvolta mellett
Eratosthenes-féle fokmérés
Almamun kalifa fokmérése
Fernel-féle fokmérés
A gömbalakú Föld coordinátarendszerének néhány sajátossága
A Föld sugarának meghatározása a szemhatár depressiója segítségével
A Föld sugarának meghatározása Dufour szerint
Ghetaldi módszere a gömbi Föld sugarának meghatározására
Klose földmérése
Egyéb módszerek
A gömbi Föld sugarának értéke
A triangulatiós módszer
Snellius, Riccioli, Grimaldi és Picard fokmérése
A Föld sphaeroidos felfogásban	436
A sphaeroid alakú Föld
A lapultság
Az ív és a sugár viszonya
Az angolok és a francziák nézete a földsphaeroidra vonatkozólag
A peru-lapplandi fokmérés
Egyéb fokmérések
A nagy franczia fokmérés	439
Talleyrand indítványa
A munkaprogramm
A munka végrehajtói
Méchaine és Delambre viszontagságai
A provisorikus méter
A fokmérés eredménye
Étalon prototype du métre
A mérésnél használt műszerek
A bázis mérése
A triangulatio
Az ellipsis egynéhány analytikai tulajdonsága	461
Az egyenes egyenlete
Két egyenes metszése
Az ellipsis egyenlete derékszögű coordinátákban
Az ellipsis egyenlete polár-coordinátákban
Az ellipsis érintője
Az ellipsis görbületi sugara
Sarkmagasság és geographiai szélesség a sphaeroidos Földön
A Föld alakjának fokmérésből való meghatározása
A legkisebb négyzetek elmélete	477
A Gauss-féle legkisebb négyzetek elmélete
Újabb fokmérések	485
A keletindiai, orosz, dán, hannoveri, keletporosz és a nagy angol fokmérés
Ezen fokmérések táblázatos összeállítása
Az ezek alapján és a legkisebb négyzetek elméletével kiszámított lapultság
A fokmérések combinatiója
A lapultság értékei
Bessel. Clarke és Listing adatai a földsphaeorid méreteire és alakjára vonatkozólag
A Föld háromtengelyű-ellipsoidos felfogásban
Összefoglalás
A méterrendszer jelentősége
Sphaerikus és sphaeroidikus problémák	496
A meridiánellipsis egy fokának és a quadrans hossza
A Föld közepes sugara
A sphaeroidikus Föld köbtartalma
A sphaeroidikus föld felülete
A geographiai és a geocentrumos szélesség viszonya
A szemhatár sugarának meghatározása
Gömbi távolságok
Gömbi távolságok kijelölése
Loxodromikus távolság
Parallelfokmérés	510
A parallelfokmérés jelentősége
A Bordeauxtól fiuméig terjedő parallelfokmérés
Európai fokmérés	512
Az európai fokmérés programmja és elért eredményei
A Föld sphaeroidikus alakjára vonatkozó ellenvélemények
Mechanikai elvek bevitele a mathematikai geographiába
Tömegvonzási jelenségek	515
A Kepler-féle törvények
A tehetetlnség axiomája
Az egyenletes körmozgás törvényei
Newton-féle axiomák
Newton-féle törvény
A newton-féle törvény fontossága és kapcsolata a Huygens- és a Kepler-féle törvényekkel
A bolygó napkörüli keringésének levezetése
Az elemi vonzások összetétele véges tömegek számára
Homogén gömb vonzása
A Föld vonzása
A Newton-féle törvény általánossága
A gömbi Föld tengelyforgásának hatása
A nehézség
A sphaeroidikus Föld tengelyforgásának hatása
A potentiál	536
A munka fogalma és mértéke
A tömegvonzás munkája végtelen kis elmozdulás mellett
A potentiál fogalma
A tömegvonzási potentiál
Az erő munkája véges elmozdulás esetén
A gömbi Föld potentiálja. Homogén gömbhéj potentiálja
Homogén gömbhéj vonzása egy belső pontjára
Gömb vonzása egy belső pontjára
A centrifugalis erő potentiálja
Az erő megkeresése a potentiál segítségével
Szintfelületek	546
A szintfelület
A szintfelületek tulajdonságai
A szintvonalak
A szintvonalak tulajdonságai
Két vonzó pont szintvonalrendszere
Két vonzó pont hatása egy harmadikra
A Green-féle tétel
Az erő és változásainak levezetése a potentiálból	551
Az erő és változásainak levezetése a potentiálból
A Laplace-féle tétel
A centrifugális és a nehézségi erő erőösszetevőinek kiszámítása
Az erő lemérése	555
Az állandó intenzitású erőmezők
A nehézségi gyorsulás meghatározása a szabad esés megfigyelésével
Az inga és mozgása
Az ingára ható gyorsulás kiszámítása
Az inga lengési idejének kiszámítása
A mathematikai, vagy eszményi inga
A másodperczinga
Az ingalengések és a nehézségi gyorsulás viszonya
Az inga lengési idejét adó képlet correctiói
Kater-féle reversiós inga
Finger-féle commutatiós inga
A coincidentiák módszere
Az ingamérések eredményei	566
Richer csillagász tapasztalata
A régibb és újabb ingamérések
Az isogramok jellemvonásai
Az ingamérések eredményei
A nehézségi mérésekből levezetett empirikus egyenlet
A Clairaut-féle egyenletek. A geoid	569
A szabálytalan Föld nehézségi potentiáljának kiszámítása
Clairaut-féle egyenletek
Szabálytalan hegy vonzási potentiálja.
A potentiálkifejtés coefficienseinek kiszámítása
A Föld tömege és sűrűsége	589
A Föld sürűségének meghatározása többféle módon
A Föld tömege
A Föld felszini és középponti sűrűsége
A la Roche és a Legendre-Laplace-féle törvény
A Nap, a Hold és a többi bolygók tömege
A Föld alakja	599
A Föld alakjának kérdése
A geoid
A geoid tulajdonságai
A niveausphaeroid
A referenzellipsoid
Egyenlő munkák felülete
Az erővonalak
A geoid kijelölése a sphaeroiddal szemben
A geoidos eltérések becslése
A geoid kijelölése a sphaeroiddal szemben	609
A mathematikai geographia alapfogalmai a geoidon
A geoid kijelölése a sphaeroiddal szemben
A modern fokmérések feladata
A Föld alakjának változása
A nehézségi változások	613
Sterneck ingájának és coincidentia-műszerének leírása
Sterneck relativ ingamérései
A Sterneck-féle ingamérésekből vonható következtetések
A Magyarországon eszközölt mérések rövid értelmezése
A nehézség relativ megmérésére szolgáló egyéb módszerek
A libellás módszer
Jolly-féle rugós mérleg
Mascart módszere
A Siemens-féle bathometer
A barometer és aneroid módszere
Egyéb módszerek. Zöllner-féle horizontális inga
Báró Eötvös Loránd módszere
A Coulomb-féle csavarási mérlegek mozgása
Báró Eötvös Loránd görbületei és horizontális variometere
A földfelület morphometriája	639
A Sonklar-féle orometriai elemek és meghatározásuk módja
Valamely alak jellemző morphologiai értékének kiszámítása
Egyenes lejtő közepes magasságának kiszámítása
Egész hegység közepes magassága
A hypsographikus görbe
A hegyoldal közepes lejtésének kiszámítása
A klinographikus görbe
Felületek területe és fejlettsége
Határfejlődés és területi tagozottság
Térfogatszámítás
Ujabb morphometriai módszer. Az oroid	657
A szintfelület fogalmának bevitele a morphometriába
Az oroid
az oroid tulajdonságai
Az oroid mathematikai kifejezése
Az oroid állandóinak meghatározása és az oroid geometriája
Perturbatiók	666
A perturbatiók vagy háborgások
A három test problémája
A perturbatiós számítások
A superpositiók elve
A mechanika általános elvei
A háborgások előállítása végtelen sorok alakjában
A háborgások értékei egy példán bemutatva
A geographiát érdeklő egyéb háborgások
A bolygórendszer stabilitása	671
A bolygórendszer stabilitásának kérdése
Laplace-féle stabilitási tételek
A bolygók keringési ideinek incommensurabilitása
Az üstökösök szerepe az állandósági problémában
A Clausius-féle hő-mechanikai tételek
A pracessio és nutatio	677
A praecessio magyarázata
A nutatio magyarázata
E mozgások mechanikai utánzása
A Föld belsejének tanulmányozása a praecessio és a nutatio alapján
A tengerjárás	681
Az árapály vagy tengerjárás jelensége
A tengerjárás statikai elmélete
A Hold és Nap árhullámának összetétele
A tengerjárás dynamikai elmélete
Thomson módszere a tengerjárás elemzésére és előre való kiszámítására
A Föld szilárd kérgének deformatiója	690
A Föld szilárd kérgének hullámzása
A Föld szilárd kérgének deformatiójára vonatkozó számítások
Összefüggés a földrengés terjedési sebessége és a földkéreg vastagsága közt
A tengerjárás mint általános érdekű kosmikus jelenség	695
A holdhegyek keletkezésénke oka
A csillagok fényváltozásai
A Kant-Laplace-féle kosmogonikus elmélet
A légkör árhullama
A Hold egyéb hatása
Egyéb földfelületi erőnyilvánulások
A földmágnesség. Előismeretek. A mágneses elemek	698
A földmágnesség tana
A földmágnesség tanának fejlődése
A mágnes és a mágneses testek tulajdonságai
A mágnesség hypothezise
A mágneses erő mérése és nagysága
A földmágneses erő és összetevői
A mágnestű mechanikája	704
A mágnestű
A mágnestű szerepe a földmágnességgel szemben
A mágneses inga lengési idejének meghatározása
Különböző testek tehetetlenségi momentuma
Segédtétel a tehetetlenségi momentumra
Mágneses absolut megfigyelések	711
A Gauss-féle magnetometer és a vele való mérés
A magnetometer lengési idejének correctiói
Mágneses elemek absolut meghatározása
Gauss-féle első és második főhelyzet
A mágnestű eltérése a Gauss-féle helyzetekben
A Dover-féle inclinatorium és a vele való bánás
A Weber-féle földinductor elve és használata
Mágneses variacziós megfigyelések	729
A mágneses elemek relativ meghatározása
A declinatiovariometer
Intenzitási variometer
Deflectoros intenzitás-variometer
Az inclinatio relativ meghatározásának módszerei
A mágneses elemek meghatározása a mágneses úti theodolittal
Az inclinatorium és alkalmazása
Az intenzitás meghatározására szolgáló módszerek
A Kohlrausch-féle helyi variometer
A mágneses erő változása és translatorikus nagysága
A mágneses elemek időbeli változásai. Földi áramok és a sarki fény	738
A mágneses variatiók
A saecularis variatio
A tizenegyévi variatio és ennek oka
A napi variatio
A variatiók évi periodusa
Az aperiodikus változások
A hazai mágneses megfigyelések
A földi áramok
A földi áramok megfigyelése
A földi áramok okai és észlelése mágneses távolbahatásaikból
A sarki fény leírása
A sarki fény magasságának meghatározása
A sarki fény gyakorisága és láthatósági határai
A sarki fény összefüggése a meteorologiai factorokkal és a mágneses háborgásokkal
A mágneses elemek térbeli változásai	756
A declinatio térbeli változása és az isogonok
Az inclinatio térbeli változása és az izoklinok
A horizontalis és összes intenzitás térbeli változása és az isodynámok
Isogon, isoklin és isodynam vonalak
A földmágnesség elmélete	762
A mágneses elemek közelítő kiszámítása Euler szerint
Gauss módszere a földmágnességi potentiál kiszámítására
A mágneses potentiál egyenlete és analogiája a geoid kifejezésével
A mágneses egyensúlyi és meridián-görbék
A mágneses elemek kiszámítása a mágneses potentiálból
Az isogonok, isoklinok és isodynamok egyenletei
Összefüggés a földmágneses helyi változások és a földkéreg geologiai és tektonikai szerkezete közt
Magyarország földmágnességi elemei
A Föld nevezetesebb mágneses variatiói
A kőzetmágnesség
A földmágnesség magyarázata	779
A földmágnesség nevezetesebb oki magyarázatai
Az északi fény főbb oki magyarázatai
A mesterséges északi fény előállítása
A Föld és éggömb ábrázolása
A vetületek általános tulajdonságai	786
A térképrajzolás fontossága
A leképzésre alkalmas coordinátahálózat
A Föld alakja a térképrajzolásnál
Gömb leképzése gömbre
A három főtulajdonság
A térképek mértéke
Gömb leképzése síkra
A beaumont-féle vetület
Perspektivikus sikvetületek	796
A perspektivitás elve
A gnomónos vagy centrális perspektivikus vetület szerkesztése és torzitási viszonyai
Mérték a gnomónos vetülethez
Az orthographikus vagy parallelvetület szerkesztése és torzitása
A stereographikus vetület szerkesztése és szögtartósága
A legrövidebb távolság berajzolása a stereographikus térképbe
A stereographikus térkép torzítása
Az extern és intern vetületek
Azimuthalis síkvetületek	820
Az azimuthalitás elve
A Postel-féle aequidistáns azimuthalis vetület szerkesztése és torzulási viszonyai
A területtartóság elve
Lambert aequivalens azimuthalis vetületének szerkesztése és torzitási viszonyai
Önkényes sikvetületek
Vetületek lefejthető felületekre	829
A hengervetületek
Perspektivikus hengervetület szerkesztése
Aequidistáns hengervetület
Az aequivalens hengervetület és torzulási viszonyai
A Mercator-féle vetület szerkesztése
Távolságok lemérése a Mercator-vetületen
Mérték a Mercator-féle térképhez
Cassini-Soldner vetülete
Önkényes hengervetületek
Flamsteed-Sanson vetülete
A Moliweide-féle vagy Babinet-féle homalographikus vetület
A kúpvetületek
Perspektivikus kúpvetület
Aequidistáns kúpvetület
De l'Isle kúpvetülete
Lambert aequidistáns kúpvetülete
Lambert-Gauss szögtartó kúpvetülete
Önkényes kúpvetületek
Bonne vetülete
A polykonos vetület angol módosítása
Polyaederes térképek
A sphaeroid leképzése	862
A sphaeroidikus Föld leképzése
A szögtartó, területtartó és távolságtartó leképzés szabályai a sphaeroidos Földnél
A térképek torzítási viszonyai	877
A tárgyalt térképek torzulási viszonyai és használhatósága
Kompenzativ vetületek
Tissot kompenzativ kúpvetülete
A térképek anyagának beszerzése	884
A térképek anyagának beszerzése
A topographiai felvételek tana
A glóbus alkalmazása	884
A glóbus
A glóbus beállítása
Feladatok megoldása a glóbussal

Témakörök

Természettudomány > Földrajz > Lexikonok, kézikönyvek

Dr. Kövesligethy Radó

Dr. Kövesligethy Radó műveinek az Antikvarium.hu-n kapható vagy előjegyezhető listáját itt tekintheti meg: Dr. Kövesligethy Radó könyvek, művek

Megvásárolható példányok

Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.

Előjegyzem