1.118.362
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát
Kisokos matematikából
| Kiadó: | Akkord Kiadó Kft.-Panem Kft. |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Varrott papírkötés |
| Oldalszám: | 608 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 11 cm x 8 cm |
| ISBN: | 963-7628-05-3 |
| Megjegyzés: | Fekete-fehér ábrákkal illusztrálva. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Tartalom
| Előszó | 11 |
| A halmazelmélet alapjai | |
| Halmazok megadása, szemléltetése, számossága | 13 |
| Műveletek halmazokkal | 17 |
| A matematikai logika elemei | |
| Ítéletkalkulus, kvantorok | 22 |
| Logikai műveletek | 24 |
| Következtetések | 29 |
| Számhalmazok | |
| A racionális számok halmaza | 31 |
| A valós számok halmaza | 41 |
| A komplex számok halmaza | 45 |
| Számelméleti alapfogalmak | |
| Osztók, oszthatóság | 56 |
| Legnagyobb közös osztó, legkisebb közös többszörös | 60 |
| Algebra | |
| Algebrai alapfogalmak | 63 |
| A hatványozás és fordított műveletei (gyökvonás, logaritmus) | 66 |
| Egyenletek, egyenlőtlenségek | 75 |
| Elsőfokú (lineáris) egyismeretlenes egyenletek és egyenlőtlenségek | 82 |
| Elsőfokú kétismeretlenes (diofantoszi) egyenletek és egyenletrendszerek | 85 |
| Másodfokú egyenletek, egyenlőtlenségek | 92 |
| Számsorozatok, számsorok | |
| A számtani, a mértani és a harmonikus közép fogalma; a rájuk vonatkozó egyenlőtlenségek | 110 |
| Számsorozatok | 112 |
| A számsorozatok tulajdonságai | 123 |
| Számsorok | 129 |
| Egyváltozós valós függvények | |
| Relációk, leképezések | 135 |
| Egyváltozós valós függvények | 141 |
| Műveletek függvényekkel | 157 |
| Függvénytulajdonságok | 161 |
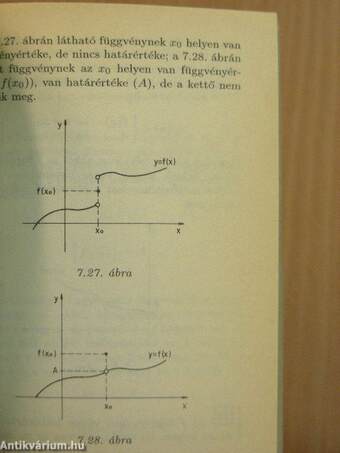
| Függvények folytonossága és a határértéke | 171 |
| Elemi függvények | 185 |
| Nem elemi függvények | 211 |
| Vektoralgebra | |
| Vektoralgebrai alapfogalmak | 216 |
| Vektorok összeadása (kivonása), számmal való szorzása | 218 |
| A vektor koordinátái | 224 |
| Vektorok szorzása | 232 |
| Trigonometria | |
| A szögfüggvények értelmezése | 241 |
| Trigonometrikus összefüggések | 250 |
| Általános háromszögre vonatkozó tételek | 253 |
| Elemi geometria | |
| Alapismeretek | 258 |
| Térelemek | 258 |
| A szög és mérése | 263 |
| Nevezetes ponthalmazok | 273 |
| Geometriai transzformációk | 276 |
| Egybevágósági transzformációk | 278 |
| Hasonlósági transzformációk | 291 |
| Egyéb transzformációk | 300 |
| Síkidomok | 307 |
| A háromszögek | 307 |
| A négyszögek | 322 |
| A sokszögek | 335 |
| A kör | 340 |
| A síkidomok kerülete és területe | 355 |
| Testek | 364 |
| Poliéderek | 365 |
| Görbealapú testek | 374 |
| A gömb | 383 |
| A testek felszíne és térfogata | 387 |
| Koordinátageometria | |
| A sík koordinátageometriája | 400 |
| A pont koordinátageometriája | 400 |
| Az egyes kooordinátageometriája | 407 |
| A kúpszeletek koordinátageometriája | 423 |
| Koordinátageometria a térben | 445 |
| A pont koordinátageometriája | 445 |
| Az egyenes koordinátageometriája | 452 |
| A sík koordinátageometriája | 455 |
| Forgásfelületek egyenlete | 460 |
| Differenciálszámítás | |
| A differenciálhányados értelmezése, a derivált | 466 |
| Deriválási szabályok | 480 |
| Differenciálható függvények vizsgálata | 485 |
| Integrálszámítás | |
| A határozott integrál | 493 |
| A határozatlan integrál | 507 |
| A határozott integrál alkalmazásai | 521 |
| Közelítő (numerikus) integrálási eljárások | 536 |
| A lineáris algebra elemei | |
| Mátrixok | 540 |
| Determinánsok | 552 |
| Kombinatorika | |
| Permutációk | 559 |
| Variációk | 562 |
| Kombinációk | 566 |
| Bevezetés a valószínűségszámításba | |
| Eseményalgebra | 569 |
| A valószínűség fogalma, kiszámítása | 574 |
| A valószínűségi változó és jellemzői | 583 |
| Tárgymutató | 589 |